Norman L. DEAN
Inertial Drive
Analog 69(3): 83-104 (May 1962)
The Fourth Law of Motion
William O. Davis
You can get away with anything provided you don't get caught while you're doing it, and you leave the system immediately thereafter! --- J. Campbell
[ Author Biography: --- Dr. William O. Davis is Director of Research of the Huyck Corporation of New York City. He was born in Buffalo, New York on November 11, 1919. He received his A.B. degree from New York University in 1939, with study at Cambridge University, England, on a Carnegie Scholarship from 1937 to 1938. He received his Ph.D. in physics from New York University in 1950.
In 1940 Dr. Davis joined what was then the Army Air Corps as a flying Cadet. At the close of World War II he was commanding the 824th Bombardment Squadron (B-24s) of the Fifteenth Air Force.
After completion of his graduate training in 1950 he became a member of the staff of the Los Alamos Scientific Laboratory as an Air Force Officer, where he worked on nuclear weapons development. From 1953 to 1957 he was Chief of Scientific Research, Headquarters, Air Research and Development Command and from 1955 to 1957 Deputy Commander of the Air Force Office of Scientific Research. It while in this post that Col. Davis initiated the Project Farside program discussed in the article "Pie in the Sky" in the August, 1961 ANALOG, the first U.S. Spaceprobe program to get instruments out into the van Allen radiation belt. And the one U.S. Space program to get there ahead of the Russians.
His last assignment in the Air Force, from 1957 to 1958, as Assistant to the Director of Laboratories, Wright Air Development Center. He resigned as Colonel from the Air Force in 1958.
In 1958-59 he was Vice President for Research, Executive Vice President and President, in succession, of the Turbo Dynamics Corporation. His research activities have covered the fields of cosmic ray neutrons, special weapons development, and the management of government and industrial research programs. ]
Fundamentally, science must be a series of successive approximations to reality. It simply is not possible to arrive at absolute truth with a finite number of investigations. Physics at the Freshman level is a very straightforward subject. Facts are well known, relationships are stated in forthright terms without equivocation, and there is little room for doubt. It takes three years or more of graduate school before it finally dawns on a budding scientist that the whole structure of science, so monumental when viewed from a distance, is a cracked and sagging edifice held together with masking tape and resting on the shifting sands of constantly changing theory. Nothing is known with any real certainty. Some things are merely more probable than others. Well-known theories and even laws turn out to be only partially confirmed hypotheses, waiting to be replaced with somewhat better partially confirmed hypotheses. If there is one thing we know about every theory in modern physics, it is that it is wrong, or at least incomplete. Sooner or later somebody will come along with a more general theory of which the old theory is seen to be a special case.
This is not a criticism of science, but merely a description of the scientific method. Like democratic processes in general--for science is necessarily a democratic process -- this method may seem a bit sloppy, and even bog down from time to time with authoritarian red tape, but it's the only method we know at the moment, and its results have been spectacular.
Progress tends to take place by a more or less random series of spurts in different fields at different times. The Laws in a given field of science will appear adequate for many years and little attention will be paid. The glamour is all in another field. Then little anomalies start showing up in engineering or scientific applications of the Laws which are accounted for by engineers through "Finagle Factors" and explained by scientists as "second-order effects." Usually, it takes a really major anomaly to generate the necessary speculation to derive a new and improved theory.
The field of Mechanics is a case in point. Euler, Lagrange, Hamilton, and Newton did such a beautiful job of synthesizing a workable theory that no further attention was paid to Mechanics for many years. Certain anomalies in astronomical data led Einstein to the Theory of Relativity, and the study of atomic physics led to the development of Quantum Theory, but the mechanics of simple everyday systems is still founded squarely on the cornerstone of the three Laws of Motion of Newton.
These Laws are usually stated in the elementary textbooks as:
First Law: Every body tends to remain at rest or in uniform motion in a straight line, unless acted upon by an outside force.
Second Law: An unbalanced force acting on a body causes the body to accelerate in the direction of the force, and the acceleration is directly proportional to the unbalanced force and inversely proportional to the mass of the body.
Third Law: For every action, there is an equal and opposite reaction.
By and large, the Laws of Motion have stood the test of time remarkably well. In spite of the newer concepts of Relativity and Quantum Mechanics, the basic meaning of the Laws has merely been interpreted, not challenged. Even then, interpretation has only been required in the case of very small or very large systems and in everyday life Newton still reigns supreme, much the distress of a host of would-be inventors.
There have been anomalies from time to time, of course, but it has normally been possible to attribute these to lack of sufficient information or understanding.
For a number of years, the author has been intrigued with a group of anomalies having to do essentially with rate of strain in materials and mechanical systems. It is well known, for example, that the strength of many materials is a function of the rate of strain. Some materials such as silicone putty, display this characteristic to a marked extent. The field of terminal ballistics is replete with odd rate of strain effects such as the tendency of long projectiles to penetrate targets by means of a series of hammer blows. There are many other examples which come to mind from almost every field of science and engineering. Generally speaking, it is very difficult to explain such effects in terms of Newtonian physics, although it has been done.
Several years ago, the importance of rate-of-onset effects in general was highlighted for the author by studies of the dynamics of the high speed pressing of paper and textiles in the laboratories of Huyck Corporation based on a theoretical study by E.L. Victory. The need to solve certain problems relating to very high speed paper machines led to the creation of a small research program involving both theory and experiment.
Interest in this field was further heightened by the discussions of the Dean Drive started by John W. Campbell in these pages in 1960. Our earlier investigations led the author to the hypotheses that the Drive, if it worked, might be explained in some way by rate-of-onset effects.
This article is a preliminary report on findings of general interest which have resulted from this research program. It is not primarily designed to explain ‘reactionless’ drives, but certain conclusions will certainly have a bearing on the evaluation of those devices. Because this is a preliminary report, there will be no attempt to offer proof of assertions as such, although it is believed that existing data will tend to confirm theoretical predictions in the areas that have been investigated after the analysis has been completed.
A speculative theory will be proposed which has been logically and mathematically explored to some extent and checked against known data in various areas of science and engineering. No claim is made that this theory has been ‘proven’ any more than any theory is ‘proven’. We do believe that this approach will shed some light on certain problems.
Let us take a moment to review the meaning of the terms describing a body in motion. First of all, a body has a position, described in terms of its distance and direction from some arbitrary point or origin. To this distance we assign the letter, s. If the body is in motion it will move a very small distance, ds, in a very short time, dt, so that its instantaneous velocity will be given by v = ds /dt .
Note that the body might move in such a way that its distance from the origin remained constant and only the angle or direction changed; it might move directly away from the origin in a straight line so that only its distance changed; or it might move in some intermediate way so that both its distance and direction change at the same time. Thus, in general v must represent a rate of change of position in any of these ways. It represents not only a speed, but a speed in a certain direction, and therefore, like the displacement, it is called a ‘vector’.
If now, we make a small change in the velocity, dv, in a small period of time, dt, the body will have an instantaneous acceleration vector given by:
a = dv/dt (1)
But, v = ds/dt, so that we can also say a = d(ds)/dt(dt), which is normally written:
a = d˛s/dt˛ (2)
An expression like ds/dt or dv/dt is called a "derivative," and therefore v is called the "first derivative" of the displacement with respect to time. Since the derivative must be taken twice to get it, we say that a is the "second derivative" of the displacement. Thus, Newton's Second Law could be written (and frequently is),
F = Md˛s/dt˛ (3)
Let us now go one step further and assume that the acceleration
is not constant. In other words, if we make a small change
in acceleration, da, in a
short time, dt, the body will have an instantaneous "surge"
given by:
ĺ = da/dt = d˛v/dt˛ = d^3s/dt^3 (4)
Surge is thus the "third derivative" of displacement. This quantity has previously been referred to as "rate of onset," "jerk," "kick," and a number of other terms. We use "surge" because it seems more appropriate to describe an action that may be repetitive or even continuous in some systems. We use the symbol ĺ because it is conventionally used an an abbreviation for da/dt.
It is possible to continue indefinitely to define fourth, fifth, and higher derivatives of displacement with respect to time. In some cases, such as very high speed impact, this may prove later to be worthwhile. In most cases, higher derivatives will probably shed little light on the problem and in the case of cyclic or oscillating motion, it can be shown that a dynamic system can be completely described with not more than three derivatives. Higher orders may be present, but can always be expressed in terms of combinations of the first three.
The class of anomalous behavior which we wish to study involves in every case the presence of surge as we have just defined it. Under conditions of constant or zero acceleration mechanical bodies or systems of bodies obey Newton's Laws reasonably well. It is under conditions of changing acceleration that difficulties arise.
The key word in our analysis of dynamic systems will be "simultaneity." The Laws of Motion presuppose exact simultaneity of action and reaction. In other words, if the force exerted by Mass #1 on Mass #2 is suddenly changed, the force exerted by Mass #2 on Mass #1 must change in the same instant to satisfy Newton's image of the universe. Einstein recognized that this condition would not be met in the case of bodies separated by astronomical distances since the change in gravitational field would have to be propagated at some finite velocity, presumably that of light, but he did not carry his investigations into the simpler field of everyday mechanics.
If it is true that two stars cannot act as a Newtonian system in less time than it takes gravity to propagate from one to the other and back, it is equally true that any real body or system of bodies suffers to a greater or lesser extent from the same problem. Newton's Laws, strictly speaking, apply only to mathematically infinitesimal particles or perfectly rigid bodies, neither of which exists in the real world.
Consider, for example, a simple steel rod one meter long which I wish to move by applying a force to one end. The instant I start to apply the force a message leaves the end of the rod as a plastic or elastic compressive wave which travels at a speed of approximately 5,000 meters/second. The compressive wave travels to the far end of the rod where it is reflected as a rarefaction and returns to the point of application of force at the same speed.
Until the wave returns, 4/10,000 of a second later <i>the rod as a whole cannot move according to the Second Law! No matter how much force is applied, the center of gravity of the rod cannot obey F = Ma in less than this time. It would be oversimplifying to say that the rod acts as though it had infinite mass during this time, since the center of gravity will be moved somewhat by compression, but for all practical purposes, the rod acts as though it had a much larger mass than it actually has.
This phenomenon is observed with all real mechanical systems to a greater or lesser extent and is normally described in the engineering textbooks as the "starting transient." Although engineers must concern themselves with starting transients in such matters as determining peak power requirements for motors, science has devoted relatively little attention to study of this phenomena, preferring, in general, to consider steady-state conditions where the Laws of Motion and the Laws of Thermodynamics may be more comfortably applied. Therefore, it is precisely with the starting transient that we will begin our investigation of the dynamic behavior of real bodies.
We have concluded that all real bodies or systems of bodies experience a starting transient when a force is applied. The particular behavior of a given system will depend on: (a) how rapidly the force is applied and, (b) the built-in delay time, or "critical action time" of the system. More exactly, we have found that the behavior depends upon how rapidly one attempts to change the acceleration applied to the body. The ultimate acceleration of the body, the "a" of F = Ma, is not what is critical; it is the rate of onset or "surge" of the acceleration which is vital.
Colonel John Paul Stapp, the USAF Flight Surgeon who subjected himself to crushing accelerations to investigate the hazards of seat ejection and airplane crashes, observed that the extent of damage to personnel and equipment depended in an important way on surge as well as the acceleration itself. In fact, today the USAF specifies limiting rates of onset as well as limiting accelerations for men and equipment. On one case, Col. Stapp estimated that the effect of a given acceleration on his body was over twice as great if applied at very high rate, than would be predicted by F = Ma !
Thus, it is not wholly illogical to attempt to solve the puzzle of high rate-of-onset anomalies by postulating that there is a force proportional to the rate of change of acceleration as well as Newton’s force proportional to acceleration itself. There is no conflict here with Newton, for Newton considered only systems where either velocity or acceleration were constant. Since his data inputs were from astronomy and since he had no instruments capable of investigating effects of changing acceleration --- effects that may occupy milliseconds or less --- this is not particularly surprising.
What form should the Equation of Motion now take if we assume a force proportional to the surge as well as a force proportional to acceleration? The simplest assumption, and one which seems to be supported by preliminary data, is that the new force is additive, in the same way that forces due to viscous drag and displacement are additive. In other words, we now write the equation of Motion:
F = Ma + Aa(superdot) (5)
Where A is a new term which we have labeled ‘intractance’ and which has units of mass-seconds. Because the solutions of the equation in some cases yield the ratio A/M as the critical action time (CAT) of the system, we have in those cases assumed that the intractance is the product of the mass and the CAT:
A = DM (6)
Let us now see how this equation of motion can be used to analyze and predict the anomalous behavior of a simple system. Starting transients normally are considered only in connection with the beginning or the end of a motion and hence are accorded no particular attention. However, there are certain types of cyclic motion where the transient behavior is continuous, or repetitive and we will see later that even certain single transients may have critical importance in understanding natural events.
First consider the simple case of a real body subjected to harmonic oscillation. To make matters easier, we will assume that there is no restoring force proportional to displacement present and no viscous damping in the system. If the applied force is simple harmonic in nature it may be expressed in the form:
![]() (7)
(7)
where f is the frequency of the vibration in cycles per second, and t is the time in seconds after the beginning of the motion. The Newtonian equation for vibration in one dimension would be:
 (8)
(8)
and the displacement of the driven body would be:
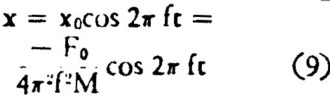 (9)
(9)
In other words, the displacement will obey Newton’s Second Law and will be exactly opposite in phase to the driving force, thus also satisfying the Third law.
However, if the body to be oscillated is real, it will not respond instantaneously, so that the rate of onset must be considered. The equation of motion then assumes the form:
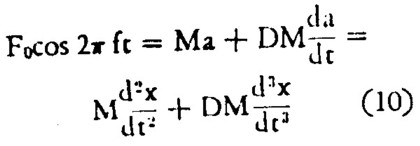 (10)
(10)
where D is the delay time, or CAT of the body and da / dt is the surge. D is assumed to be constant.
This equation has the solution:
![]() (11)
(11)
where
![]() (12)
(12)
and
 (13)
(13)
where Z is a sort of complex impedance and
![]() (14)
(14)
The important feature to note in this solution is that the amplitude of the oscillation is less than predicted by the Newtonian equation and even more important, there is a phase angle between the driving force and the displacement, even in the absence of viscous damping. This solution demonstrates the most significant characteristic of real bodies, to wit: not only is displacement somewhat less than Newton would predict for a given force, leading to an increased apparent mass, but reaction is no longer exactly opposite to the applied force: there is a phase angle which will be larger the longer the CAT of the system! Action and reaction are not simultaneous!
A technical paper will be published in the near future which will present a more general discussion of solutions to the equations of motion. The solution presented here will serve only to show the effect of CAT in a system under the simplest situation. The disastrous effect on the theory of mechanics of the existence of CAT in real bodies may be realized at once when we consider a system so arranged that the CAT is not the same in all directions.
If, for example, we build a mechanical oscillator such that the CAT is short compared to the period of oscillation in one direction, the mass will appear to be approximately Newtonian and the phase angle of reaction will be negligible when the oscillator is moving in that direction, If we now change the system to make the CAT much longer during the time the oscillator is moving in the opposite direction, the mass will appear to be greater and the phase angle larger, even though the total applied force is exactly the same I the two directions. Thus there will be a net unidirectional acceleration of the driven mass in the direction of the least apparent mass even though the applied force is balanced!
This conclusion is merely a logical consequence of the existence of a force proportional to the third derivative. We have not yet, of course, considered how such a behavior could be possible in terms of physical reality.
In recent years a number of ‘reactionless’ drives have been proposed and some demonstrated, including the controversial Dean Drive. To the extent that any of these devices have produced useful thrust, they presumably have embodied this principle. It is not the purpose of this article to attempt to explain the operation of these systems as such, nor to claim that any of them are practical devices. However, an analysis of the possible compatibility of some form of mechanically reactionless drive with the body of known data from the past may help shed some light on deficiencies in present theory and, hopefully, lead to some useful applications.
If a device of this kind operates, what has happened to the Laws of Conservation of Momentum and Energy? Actually, the situation is no worse than it once was in the field of electricity. It was sincerely believed a century or so ago that it would be impossible to do work with alternating current without violating the Conservation of momentum, since the average current was zero. Although the current in one direction is balanced by an equal flow in the opposite direction, the flows are not equal and opposite simultaneously and thus work can be done. Furthermore, when all else failed, radiation was invoked to preserve the Conservation of Momentum.
We are going to try the same approach. Let us again consider the case of a real body, having mass M and constant CAT D, moving in one dimension, and let us calculate the kinetic energy of the body. If the force is applied over the distance between two positions X0 and Z1, during a corresponding time interval, t0 to t1, then it can be shown that:
 (15)
(15)
where v is the velocity and a the acceleration in the x-direction.
It will not be necessary to go into the calculus involved. The important point is that only the first term on the right-hand side is Newtonian. The second two terms represent the portion of the energy that has not been converted to kinetic energy because of third derivative effects. This portion of the energy, in keeping with the terminology applied in modern nuclear physics to particles which exist in the nucleus for too short a time to violate the law of the Conservation of Energy, we have called the ‘virtual energy’. Thus this equation expresses an amendment to the Energy Conservation Law by a new ‘Principle of Virtual Energy’. If a force proportional to surge exists, then a logical consequence is the existence of such ‘virtual energy. We will continue to explore the question of whether this makes sense in terms of the real world.
Let us see what the presence of virtual energy in a system implies. First of all, if the acceleration is constant the sum of the virtual energy terms is zero and the equation becomes Newtonian. The equation is not readily soluble for an arbitrary variation of acceleration with time but a simple example will demonstrate the principle. Let us assume a constant surge as such that the acceleration varies according to:
![]() (16)
(16)
For the sake of simplicity let us assume that we are describing a rocket during takeoff so that the initial displacement, velocity, and acceleration are all zero and t0 = 0. We will also ignore the presence of the earth’s gravitational field, since the conclusions will not be affected. One can then find the solution that at time t, the virtual energy is given by:
 (17)
(17)
This means that the kinetic energy at t1 will be too small by this amount. The rocket will have acted as though it were heavier than its true weight! What has happened to the energy that has been lost?
Now it is necessary to go back and make some postulates. A moving electrical charge creates a magnetic field. Einstein, in his general Field Equations assumes that a moving gravitational ‘charge’ or mass will also produce a field. The predicted strength of such a field is extremely small for any reasonable velocity, smaller in general than the gravitational field due to the mass alone. Any radiation resulting from the interaction of the gravitational and ‘inertial’ field --- in the same way that electromagnetic radiation results from the interaction of the electric and magnetic fields --- is thus so small as to be negligible in any practical system.
Although all of the reasons cannot be developed here, I believe it is more reasonable to postulate an ‘inertial’ field due to acceleration of a mass rather than simply due to its velocity. It is as though the fundamental ‘charge’ were momentum, Mc, instead of simply the mass, M.
It is possible in this light to point immediately to the gyroscope as a well-known example of an inertial field. Mathematically, the ‘angular momentum’ of a gyroscope is calculated from the motion of the mass in the wheel in exactly the same way as the magnetic field of a solenoid is calculated from the flow of current. Mathematically, then, ‘angular momentum’ may be said to be identical with ‘inertial field’ in this case, and we will prefer the latter terminology. Anyone who has felt the resistance of a gyroscope to precession will know that this type of ‘inertial field’, if that is what it turns out to be, is far from negligible. The forces involved may be very large with a heavy wheel rotating at high speeds. Since there exists a constant centrifugal acceleration in a gyroscope running at constant speed, any attempt to precess the device must automatically result in a ‘third derivative’ reaction force, since the acceleration is being changed.
Based on this example it can now be seen that the coefficient of the third derivative or surge term in the Equation of Motion must represent the resistance of the system to a change of inertial field, in the same sense that self-inductance represents the resistance of a coil to a change of magnetic field. We have discussed a case where we assumed that this coefficient was the product of the mass and the CAT of the system. This is not necessarily true of all systems, so that we choose to define this coefficient more generally in relation to the inertial field as ‘interactance’ of a system. Thus the force due to rate of onset may be defined as the product of the intractance and the surge.
The well-known concept of a limiting velocity of propagation for energy in any form established by Einstein is a direct embodiment of the intractance of real systems. In fact, viewed from another point of view, it is precisely the intractance of a system which requires that propagation velocity be limited. If energy could propagate at infinite speed, then it would be possible to change the energy of a system in zero time.
Now it is possible to visualize a completely new type of radiation resulting from the existence of this type of inertial field. If an electron radiates electromagnetic radiation when it is accelerated, then clearly we will now expect a mass having intractance to radiate gravitational-inertial radiation when it is subjected to surge. It is in fact my postulate that the flux of such radiation from a system is proportional to the rate of change of virtual energy. Based on this assumption, the energy which has failed to appear as kinetic energy or potential energy in the example of the rocket we discussed, has left the mechanical system in the form of gravitational-inertial radiation, as we have defined it.
For obvious reasons it will not be practical to go into the mathematical steps taken to arrive at this conclusion, but once again we have followed a logical course starting from the assumption of a third derivative force. It is interesting to note that the new radiation, if it exists, will have radically different characteristics than electromagnetic radiation, at least as it is now described. First of all, it is not dipole radiation, but more like the radiation from an ‘end-fire’ antenna. Secondly, each period of changing acceleration produces a ‘quantum’ of radiation equal to the change of virtual energy, so that the emission is not continuous.
The consequences of this behavior will have to be explored in more detail in the future. It is even possible that this approach may shed some light on the quantum nature of electromagnetic radiation. For example, we have considered the hydrogen atom in an excited state. By writing the equations of motion for an orbiting body with intractance, it can be shown that when third derivative effects are considered the angular momentum is not initially constant! In fact the equations show that a body first placed in orbit contains a significant transient term in the expression for its angular momentum which ultimately decays to a constant with time.
Furthermore, the energy lost during this decay disappears entirely from the mechanical system and can only be accounted for by some form of radiation! Thus if the electron of a hydrogen atom were excited with additional kinetic energy, out theory would predict the radiation of a quantum of energy during this decay time. It is therefore possible that the quantum condition is a perfectly logical consequence of thee existence of intractance in real systems, and that thus quantum theory can be derived from Newtonian physics!
During this brief discussion of the application of our theory of real dynamic systems to nuclear physics some reference should be made to the upwards of 40 new nuclear particles which have been postulated in recent years. Since many of these particles have been postulated to explain an apparent violation of the Conservation of Momentum during some very brief time period --- brief even by nuclear standards --- it is possible that the Principle of Virtual Energy may offer an alternative explanation in many cases.
Quite apart from the possibility of inertial radiation, several conclusions may now be drawn, at least on a tentative basis. When computed including intractance, the solutions to the equation of motion indicate that very large systems should tend to be unstable, unless the mass in the system is very large. This conclusion, for example, may have a bearing on the theory of the expanding universe. Furthermore, it suggests that the application of thermodynamic analysis to large systems should be re-examined. Thermodynamics relates to systems in equilibrium and simultaneity is obviously important. If gravitational waves propagate at the velocity of light, which is by no means certain yet, then the CAT of the observable universe is roughly 12 billion years and simultaneity cannot be defined for the complete system in less than that time. Thus it should be perfectly possible to reverse entropy in a local area and not have to pay the piper for a very long time!
We come now to a consideration of what must be the Fourth Law of Motion. There will obviously be several alternative expressions. Mathematically, what seems to be critical in systems with intractance is the rate of change of energy, so that the Law is perhaps best expressed in these terms: The energy of a given system can only be changed in some finite length of time depending n the system, and never in zero time.
Similarly, one can suggest an expression for the Fourth law of Thermodynamics, to wit: Systems can only be considered to be thermodynamic in nature of time periods large in comparison to their CAT. In other words: You can violate the first three Laws, providing you don’t get caught while you’re doing it!
At this point, it is proper to ask the question: Is there any real evidence for this theory, and if it is true, why haven’t these phenomena been obvious for some time?
First of all, rate of onset effects per se are well-known and their existence is hardly controversial. The entire field of shock and vibration gives signs of supporting our conclusions. In general, mechanical systems do not possess the simple resonance characteristics that Newtonian theory would predict. The existence of intractance permits many more modes of resonance since there are now four terms of interaction in the equation of motion for a system restoring force instead of three. This permits a much greater number and variety of resonances to occur.
The discovery of the existence of ‘virtual particles’ in the atomic nucleus, which appear to violate the Conservation of Energy, is an important addition to the list of anomalies which suggest the validity of the theory. Under the assumption that the theory is correct, it is possible to derive the quantum condition from the planetary model of the atom. In short, wherever the theory would predict certain behavior, there are indications that the behavior is present. Obviously, the mere fact that an equation gives correct results does not mean the theory is correct. The model must also make sense.
Most obvious embodiments of third derivative theory are associated with high rates of onset, impact, or strong vibrations. Under these conditions, it is very hard to make measurements. It is hard to find accelerometers, for example, which have response times sufficiently short to permit proper observation. For another thing, a system running in a continuous or intermittent transient mode tends to create very large internal forces which are very destructive. It is hard to maintain a system at its proper operating point for a long enough time to make observation. It is highly probable that most data of this type of behavior consisted of observations of the type, ‘Then the machine broke down for no known reason’, or ‘Witnesses stated that the wing suddenly broke off the airplane’.
Evidence for the existence of inertial radiation is not quite as plentiful. The concept of gravitational waves is not a new one, and in fact is implicit in the weak-field solutions of the Einstein General Field Equations, known for 40 years. On the other hand, the type of gravitational-inertial radiation predicted by our theory is quite new since it is presumed to be a consequence of surge rather than simple acceleration. The magnitude of the Einstein radiation is predicted to be so small as to defy detection, but the radiation described here should be clearly observable under the right conditions.
For example, the success of one of the proposed ‘reactionless’ drives would strongly tend to confirm the existence of the radiation. At the same time, if the radiation is generated it should be detectable, and sooner or later a ‘Hertzian’ experiment will have to be performed. A number of experiments are now underway in our laboratories at Huyck Corporation which we hope will provide confirmation in the near future. Preliminary tests have produced favorable qualitative results, but data has not been sufficiently accurate to permit a proper statistical correlation. We hope to correct this situation with new instrumentation by the time this article appears.
In addition to the author, a number of individuals have played key roles in the Huyck Dynamic Systems Project. The experimental work was performed at the Huyck Research Center at Milford, CT, under the direction of Mr G. Henry Stine who also contributed a number of concepts to the theory. Theoretical calculations and analytical studies were performed by Mr E.L. Victory. Certain specialized instrumentation and general consultation were provided by John W. Campbell, uder a consulting agreement, and overall professional review of the theoretical and experimental programs has been given by Prof. Serge A. Korff, of the Physics Department at New York University. We are also deeply indebted to Dr O.G. Haywood, Vice president of Huyck Corporation, for technical and moral support.
Obviously, there are an almost unlimited number of fields where the consequences of this theory might be explored. Validation, if ever, will probably result from may experiments in many fields. We cannot perform them all. We intend to continue our own research program and will be interested to hear of the results produced by other groups.
Science, as we said, is a series of successive approximations to reality. Here is another approach. Let’s find out if it’s a better approximation.
Analog (October 1962): ‘Brass Tacks’
Dear John [Campbell]:
Dr Davis and I were finally able to settle our arguments over the equation that appears in Figure 4 of our article entitled ‘The Fourth Law of motion’ in the May issue of Analog only after I studied the equations --- which are incidentally the Lagrangian form of the third derivative Law and the differential equation of the angular motion of an orbiting body --- as they were recorded by the camera.
After noticning the missing dot that was not on top of the O on the second term of the differential equation, we realized who was right.
May I also correct equation 17 by squaring the term a(dot)o ---
E.L. Victory, Huyck Corporation, NY.
