Motional Electric Field
New Horizons In Electric, Magnetic & Gravitational Field Theory
by William J. Hooper
(B.A., M.A., Ph. D. (University of California Berkeley); President & Director of Research, Electrodynamic Gravity, Inc.; Professor of Physics Emeritus, Principia College.)
__________________________________________
Table of Contents
Introduction: New Horizons in Field theory
Chapter 2: The Electromagnetic Force Equation
Chapter 3: Experimental Confirmations by Electrostatic Shielding
Chapter 4: The Motional Magnetic Field
Chapter 6: Anti-Gravity & Electrical Power
Chapter 7: Some Confirming Experiments
This book is dedicated to Mr. And Mrs. Warren W. Gibson, who have made it possible financially to carry on the last two years of fruitful experimental work. The devotion and dedication of Mrs. Gibson (Fran) to this project, serving as secretary and Research Assistant, has provided a flame which has kept it aglow to its present status.
"It appears to me, that the study of electromagnetism in all its aspects has now become of the first importance as a means of promoting the progress of science." (James Clerk Maxwell: Treatise on Electricity & Magnetism, Vol. 1, Pref., p. vii.)
Nearly everyone believes that gravity is a force emanating from matter, but just how, just why, nobody seems to know! In the science of physics much is known about electricity and magnetism, but of gravity, nothing really, with the exception of the inverse square law of Sir Isaac Newton, which we know gravity obeys.
This treatise presents newly discovered unique and startling properties of one of our induced electric fields. It gives this field a new status among our field forces. Its unusual properties are possessed only by gravity. While it is too early to claim complete identification of this field and the gravitational field, the similarities are amazingly alike.
Electricity and Magnetism were once two separate sciences. In 1820, Hans Christian Oersted observed that magnetic flux was always looped about a current-carrying conductor. This discovery served to unite the two sciences of Electricity and Magnetism into one, that of Electromagnetism.
During World War II the writer, working on an invention for a "drift and ground speed meter for aircraft", arrived at a plan for utilizing the vertical component of the earth's magnetic field. If the voltage induced between the ends of two oriented linear conductors traveling horizontally across the vertical component could be measured within an aircraft, a self-contained meter, independent of ground instrumentalities, would be forthcoming. The plan was reviewed by the U.S. Bureau of Standards, and its workability confirmed under a certain restriction. It was stated that the device would be inoperable within a conducting cavity such as a metal-clad aircraft. Our textbbooks have taught us that when a linear conductor moves with a velocity V across a magnetic flux of intensity B, an electric field of vector intensity VxB is induced within the wire and gives rise to a voltage at its terminals. This electromagnetically induced electric field, often called a motional electric field, we have been taught, would be electrostatic in character, that is, identical and indistinguishable from an electric field arising from charges of electricity. We know that radio tubes, silvered on the inside, shield the interior from stray electrostatic fields. In the same way, it was explained, such a drift and ground speed meter within a metal-clad aircraft would be shielded from the electric field induced in a conductor by motion across the vertical component of the earth's magnetic field. This explanation was a jolt to the writer. How could we know, without experimental evidence, that such would be the case? This presented a great challenge! Some of the foremost thinkers in physics were consulted. It was discovered that there was no experimental evidence to support the popular belief held by physicists that the motionally induced V x B field was electrostatic in its fundamental character and therefore subject to shielding. It will be shown how, step by step, the writer has been guided over a period of 20 years to experimental means which at last reveal experimentally, beyond all doubt, the beautiful unique properties of the motional electric field. It is not electrostatic! Its immunity to shielding, magnetic or electrostatic, is the exciting property which it shares with the gravitational field and thereby indicates their kinship. By a general theorem in electric field theory we know that a non-uniform B x V field must also act attractively on matter! Thus the motional electric field has acquired a status which makes it quite unique.
Guided by theory the inventor has built a generator of the B x V field which projects its field into the surrounding space. The writer calls this artificially generated field Electrodynamic Gravity because it simulates gravity. Although utilizing principles of magnetic field superposition and electromagnetic induction, the product field, B x V, like the gravitational field displays no evidence that magnetism plays a part in its generation. Likewise it is free of electrostatic characteristics. Although magnetic flux is moved by the generator, there are no mechanically moving parts.
The guiding concept employed by the inventor was first set forth in 1957 by E. G. Cullwick (Electromagnetism & Relativity, p. 245, Longsman Green & Co.). His research had led him to the conviction that the magnetic flux loops discovered by Oersted were actually in motion along the linear conductor in the direction of the electron current giving rise to it, and moved with the electron drift velocity. Our motional electric field generator demonstrates the correctness of the foregoing prediction. Its operation makes use of this movement of flux to generate the B x V field in space about the generator. This confirmation of Cullwick's prediction is an experimental contribution to modern electronic theory and it has all the earmarks of being the welding link which ties gravitation to electricity and magnetism. The oersted flux, first its discovery, and now the discovery that it moves with the electron drift velocity giving rise to it, thus holds a unique role in the process of welding the three sciences into one.
The new generator affords useful instrumentation for directly measuring electron drift velocities in metals, as well as experimentally determining the number of electrons available at various temperatures. Thus, it provides a new experimental method f investigation into the realm dealt with by the Fermi-Dirac statistics. Theoretically, this device holds exciting possibilities of great utility at very low temperatures. If sufficiently intense fields can be obtained by the use of superconducting wire in our generator at low temperatures, as we have good reason to believe is possible, the phenomenon of attraction and polarization of materials by this field can be studied. This would immediately bring into the realm of possible experimental demonstration such effects as weightlessness, artificial gravity, and anti-gravitational effects. This achievement, the writer believes, will be no more difficult of attainment than that which has already been demonstrated experimentally.
Should success follow the forthcoming planned cryogenic (low temperature) experiments and we find that very intense B x V fields can be generated and identified with the gravitational field, the promise of utility to humanity would be beyond all description. Free electric power from the earth's gravitational field would be obtainable anywhere, under the sea, on earth or neighboring space, on the moon or the planets! Gravity-free laboratories on earth, and artificial gravity in spacecraft --- these are some of the possibilities! With such promises on the horizon it is difficult for the writer to rest on his oars for one minute. This treatise therefore goes forth with "Great Expectations!"
Sarasota, FL (December 1969)
New Horizons In Field Theory
Forty years have passed since Max Mason and Warren Weever wrote in their celebrated book, The Electromagnetic Field (1 ~ p. xii, Univ. of Chicago Press, 1929):
"The great scientific task of the next 50 years is the development of a new electromagnetic theory. It is impossible to forecast the form such a theory will take, so greatly are we prejudiced by our present views. It will, however, doubtless be based on a quantitative description of the individual behavior of charges"
The new physics under the leadership of such men as Einstein, Planck, Heisenberg, Schrodinger, and Bridgman, has produced a series of kaleidoscopic changes in classical concepts. The contributions of the first four of these five men have been well incorporated into our modern textbooks. It is the work of Bridgman, his philosophy as embodied in "The Logic of Modern Physics" (2 ~ MacMillan Co., 1928), and paraphrased as "The Operational Viewpoint", which has to a large extent inspired this treatise, and provided a beacon of illuminated thinking to guide contemporary physicists in the development of new ideas. What Bridgman has done is to show us how the advent of relativity theory has made it necessary to take cognizance of the fat that new phenomena spring into existence as the result of introducing into an experiment nothing more than motion or a change in motion. We must be aware of assuming that because of the fact that similarities exist between old and new phenomena that they are necessarily equivalent. To be specific, let us again turn to Mason and Weaver:
"It cannot be urged that it has been shown experimentally that moving particles and changing currents are rigorously equivalent as regards induced electromagnetic forces. It is very easy to let the notation carry the burden of the argument and to hold that the value of curl E s related to the rate of change of B in every case in the way stated by the equation (curl E = -?B/?t). It is very important to point out, however, that by doing so one may be overlooking something of fundamental physical importance." (3 ~ ibid., p. 257)
It is this "something of fundamental physical importance" which is overlooked when the so-called "principle of equivalence" is applied without rigorous examination and analysis. This is the very essence of Bridgman's thesis.
There is no evidence that the subject matter of electromagnetism, since its earliest inception, has ever been given the Bridgman treatment. If we desire to keep our future growth on solid scientific ground, we are faced with the necessity of review and revision of old and new concepts which dominate thinking in the direction of its inevitable expansion. We need much to learn how "greatly are we prejudiced by our present views". In order to make way for the next great breakthrough in physics we must first come face to face with facts that reveal how greatly our present concept of fields is restricting our thinking and limiting our achievements.
An example of one of the greatest blind spots in current popular field theory will illustrate this point. This blind spot, due to an assumed concept, has been upheld by some of our most brilliant mathematical physicists. So dogmatic and completely certain of the accuracy of his position was one that he contributed the following jingle with which to support his conviction:
"There is but one God Allah, And Mohammed is his prophet! There is but one electric field E, and Maxwell is its prophet!" (4 ~ J. Stepian, "Electrostatic or Electromagnetically Induced Electric Field?"; Scientific Paper 1451, Westinghouse Research Laboratory, 7-14-49)
That nature has provided us with but one field agency which accelerates electrons, one electric field, and that one electrostatic in its fundamental character, is perhaps the greatest of all our current prejudiced and erroneous views. None of Faraday's famous experiments show or prove the existence of but one electric field in nature. It is Maxwell's translation of these experiments into the language of mathematics that bear the tacit assumption of only one such field. But Faraday left us a word of warning:
"and considering the constant tendency of the mind to rest on an assumption, and, when it answers every present purpose, to forget that it is an assumption, we ought to remember that, in such cases, it becomes a prejudice, and inevitably interferes, more or less, with clearsighted judgment." (5 ~ Phil.Mag., 1844)
It will be shown with experimental and theoretical proof that this assumed and prejudiced view is incorrect. Indeed, it is as obsolete as the concept of the atom as being a single indivisible particle, and as obsolete as the concept of a single atom for each element. It is as unrealistic as were the arguments of the famous Professor Simon Newcomb, recipient of honorary degrees from ten European and seven American universities, who was demonstrating mathematically that man could not fly, while the Wright brothers were assembling their aircraft at Kitty hawk. Simply because it can be shown mathematically that an electrified particle will trace identical trajectories in each of two types of fields, is no proof that these fields, these accelerating agencies, are equivalent and identical. Penetrating properties of fields, rendering them immune to shielding, possessed by some and not by others, have no mathematical representation in such so-called proofs, hence the proof is not rigorous because it does not include all the field properties.
A second modern prejudice, an assumed concept, which has gained considerable popularity, is one which states "the whole concept of a magnetic field is a fiction." (6 ~ P. Moon & D.E. Spencer: "Electromagnetism Without Magnetism: An Historical Sketch"; Amer. J. Phys., vol. 22, p. 120, 1954)
By combining two conceptual prejudices, "one electric field" (or its equivalent, electric charges only) and "no magnetic field", Moon and Spencer have produced what they call "A New Electrodynamics" (7 ~ J. Franklin Inst. vol. 257: p. 369, 1954) which appears on the surface to have revamped the whole picture of electromagnetism, in which no reference is made of fields, and the formulation is in terms of charges and their motions only. It would appear upon first examination that the success of their endeavors would constitute a basis for establishing the verity of the two basic assumptions. But this is not the case, as will be shown. The Bridgman treatment of Maxwell's equations clarifies the paradoxes and ambiguities previously associated with them and in so doing it retains the intrinsic values found in electric and magnetic field concepts ( 8 ~ P. Moon & D.E. Spence: "Some Electromagnetic Paradoxes", J. Franklin Inst., vol, 260, p. 373, 1955). Both the Maxwell equations and the "New Electrodynamics" formulation take on new meanings when analyzed in the light of the Operational Viewpoint urged by Bridgman. We will go into this subject in the next chapter.
Wile Moon and Spencer claim that the complete elimination of all reference to electric and magnetic field concepts in their formulation brings it to "a closer contact with reality", to the writer, this constitutes rather a fleeing from the reality of fields by burying one's head in sand, like an ostrich, wherein only sand particles can be seen, and one's body remains in a variety of teeming dynamic forces.
The idea that magnetism may not have physical reality because electric currents which give rise to certain aspects of it may be replaced in the equations by moving charges has been given much consideration. Page and Adams in discussing elementary charge and the force equation state:
"It is often stated that no magnetic charges exist in nature, and that therefore the terms in ?H in this equation are without physical significance. On the contrary, we shall show that, if every elementary charged particle contains electric and magnetic charges in the same ratio, no electromagnetic experiment can reveal the value of ? --- therefore the field equation and the force equation become identical in form with the equations obtained on the assumption that only electric charge exists in nature. There is no experimental evidence, therefore, to justify the common assumption that only electric charges and no magnetic charges are present in the world of experience. If the reverse were true, or if electric and magnetic charges occurred combined in any fixed ratio, all electromagnetic phenomena would take place in exactly the same way. No electromagnetic experiment would reveal the proportions in which the two types of charge might exist." (9 ~ Leigh Page & Norman Adams: Electrodynamics, pp. 210-211, Van Nostrand & Co, 1940)
The concept of electric and magnetic fields possessing intensities and directions, susceptible to direct experimental measurement and mapping, is one of the most fundamental and elemental realities of electromagnetism. True it is that perplexing and incongruous problems in field theory, heretofor seemingly unsolvable, have plagued it, and indeed these problems are largely responsible for the current trend to avoid field theory, especially magnetic, wherever possible. It is right in this area that Bridgman's Operational Philosophy comes to our rescue and affords a solution which is both satisfying and illuminating.
Electric and magnetic fields are manifestation of force, and force is always associated with energy. Our understanding of the energy nature of electric and magnetic fields up to the present time appears clouded and uncertain. A clear adequate description has not been found by the writer in any contemporary text. In place thereof is found confusion worse confounded. In order to fully comprehend the significance of this treatise we must have some acquaintance with the present status of our knowledge of fields, both energy-wise and otherwise. A glimpse of this state of affairs may be gained from a few quotations from The Electromagnetic Field (10 ~ Mason & Weaver, op. cit., pp. 266-269). Speaking of the special density of electric and magnetic energy and of the Poynting Vector which measures the flux of energy at any point, we read: "The authors do not pretend to understand these concepts, but discuss them as adequately as they are able". They further say that they "are not able to ascribe any significance whatever to the phrase 'localized energy'". Nothwithstanding these views, they state, "The hypothesis of a spacially distributed electrostatic energy of volume density ha, however, played a large role in the development of electromagnetic theory" (11 ~ ibid., p. 162). And again, "in both electrostatics and magnetostatics, energy densities in space have, to be sure, been calculated" (12 ~ ibid., p. 269). It is an object of this treatise to completely clarify this area of electric and magnetic field energy.
Energy, in the many forms it assumes, appears today to play a leading role in the great drama of physical science. Whether it is kinetic or potential, mechanical, electric, magnetic, electromagnetic, binding energy of nuclear structure, or any other of its myriad manifestation, it is some form of energy, pure or bottled up in particle form, which we encounter and cognize at every turn in this physical world. Everything in the material universe is some form or manifestation of energy.
In the light of fundamentals it would seem most natural that a proper scientific description and classification of anything would include terms which reveal its energy nature, or status with respect to energy. In a comparison of one thing with another, one recognizes as a mere self-evident truism the fact that for any two things to be identical in nature, they must necessarily be identical from an energy standpoint, and this truism especially applies to force fields, both electric and magnetic.
This treatise will especially concern itself with one of the most important underlying properties of one of our electric fields, the "motional electric field B x V" and its immunity to shielding. It will present new theoretical and experimental knowledge which must have consequences of vital importance to the science and philosophy of modern physics. The picture presented will be based entirely upon conceptions of electromagnetic theory which are found in complete agreement with experiment. This picture, it is believed, will reveal not only the cause of many of our difficulties, but the way out of them. It will reveal a vista of new opportunities for research. It is confidently believed that as a result of the clarified picture thus attained, new horizons in field theory are in the offing. A glimpse of these horizons, together with an electromagnetic theory of gravitation leading up to the derivation of Newton's Inverse Square Law, will be presented with experimental proposals for its verification. Finally the subject of antigravity will be discussed and, in the light of this thesis, how a practical approach to this problem is clearly indicated with its thrilling possibilities.
Fundamental Fields
Webster defines science as "knowledge classified and made available in the search for truth". A correct classification of knowledge thus becomes the basic foundation of a science. The word classification has been underlined by the writer, because of its great importance. A wrong classification of anything can result in greatly impeding the progress of the branch of science in which it exists. Thus great treasures in science can be hidden and obscured for ages until some prospector comes along and reveals its true nature. A critical survey of the present status if electrodynamics reveals a considerable number of electric and magnetic fields which are brought into being by operations which are unique and seemingly unrelated. So entrenched is the present tacit assumption of physicists that nature has provide nature with one and only one electric field and one and only one magnetic field that no pioneer has as yet attempted to seriously penetrate this prejudice and venture into the possibilities of classification which might bring law and order to some of our current problems.
The advent of relativity theory was instrumental in forcing physicists to reexamine and alter many of their most cherished and fundamental concepts in physics. Consdier, for instance, the concept of time. None other than the great Sir Isaac Newton has defined time, in his Principia, in the following manner:
"Absolute, True, and Mathematical Time, of itself, and from its own nature flows equably without regard to anything external, and by another name is called Duration."
Bridgman points out with great clarity that f we examine the definition of absolute time in the light of experiment, we find nothing in nature with such properties. By example after example he points out that many of the stumbling blocks which have clogged the progress of physics, and then he does something about it. He has contributed what is called the Operational Viewpoint as a guiding beacon to enable us to avoid making these kinds of mistakes in the future. In brief, he tells us what we should define and classify our concepts in terms of the operations which are necessary in order to detect and measure them, and not in terms which have no counterpart reality in nature, no direct experimental evidence to support them. Only as we do this, he points out, can we avoid treacherous pitfalls and embarrassments in the future growth of our science. He states, "It is evident that if we adopt this point of view toward concepts, namely that the proper definition of a concept is not in terms of its properties but in terms of actual operations, we need run no danger of having to revise our attitude toward nature. For if experience is always described in terms of experience, there must always be correspondence between experience and description of it, and we need never be embarrassed, as we were in attempting to find in nature the prototype of Newton's absolute time" (13 ~ Bridgman, op. cit., p. 6). While stating that "operational thinking will at first prove to be an unsocial virtue", he nevertheless predicts that, "In this self-conscious search for phenomena which increase he number of operationally independent concepts, we expect to find a powerful systematic method directing the discovery of new and essentially important physical facts" (14 ~ ibid., p. 224).
The writer has classified operationally the three most prominent electric and the three most prominent magnetic fields which we find in nature. They are as follows:
Fundamental Electric & Magnetic Fields (m.k.s. units)
(1) Ec = Qr/4 pi eor3
The electrostatic or Coulomb field arising from the presence of charges
(2) Em = v x Bs
The motional electric field which acts on charges traveling with velocity V across a magnetic induction Bs. This field is produced by flux cutting and should not be confused with Et arising from flux linking
(3) Curl Et = ?B/?t
or Et = ?A/?t

The electric field Et, in this formula arises from flux linking, or transformer electromagnetic induction discovered by Henry and Faraday. In this field B changes intrinsically with time. A is the magnetic vector potential.
(4) Curl Hs = J
This magnetostatic field H arising from a conduction current density J within a conducting medium was first discovered by Oersted. It is at rest with respect to the current circuit source producing it.
(5) Hm = -v x Dc
The motional magnetic field arising from relative velocity v with respect to electric charges producing the electric induction Dc.
(6) Curl HR = ?Dc/?t
![]()
The magnetic field HR surrounding a changing electric induction called a displacement current. This magnetic field plays a prominent part in the production of electromagnetic radiation. It was first theoretically predicted by Clerk Maxwell.
Particularly illuminating is the analysis of Cullwick with respect to the salient operational differences in the sources of the three types of electric field Ec, Em and Et (15 ~ E. Geoffrey Cullwick: The Fundamentals of Electromagnetism, p. 285; Cambridge Univ. Press, 1949). In brief, he pictures them as follows.
All electromagnetic phenomena applied in electrical technology have, as their fundamental basis, the mutual forces experienced by electric charges, and we have seen that these arise in three ways:
Ec ~ Two charges experience mutual forces in virtue of their positions. This is the electrostatic force of attraction or repulsion.
Em ~ They experience additional forces in virtue of their velocities. Thence arise the forces experienced by a conductor carrying a steady current in a constant magnetic field, the forces between current-carrying conductors, and the induction of en emf in a conductor moving relatively to the source of a magnetic field.
Et ~ They also experience additional forces by virtue of their accelerations, from which arise the induction of an emf by transformer actions, and electromagnetic radiation of energy.
The thing we are especially interested in, in this thesis, is that each of these unique operations with charges brings into existence a new force field which will act upon charges of electricity to accelerate them. The intensity of an electric field is defined at a point as the force per unit of charge will be exerted. The great mistake of the past has been the assumption that each of the above accelerating agencies are, in their intrinsic physical natures, in every way equivalent and identical since they each produce the same end product, the acceleration of a charged particle. Now in my human experience I may desire to move across a lake in a boat. As accelerating agencies I may select several which are one unique: (a) a set of oars, (b) a sail, (c) an outboard motor, (d) an engine-driven air propeller.
There is no question with respect to the uniqueness of these agencies in spite of the fact that each one produces the same end result --- namely, a force on the boat. Because we cannot cognize directly the unique accelerating agencies in electrodynamics by means of the five physical senses, they have been assumed to be all alike in nature, in spite of the known fact that operationally they arise from manipulations which are as uniquely different as in the case of the three accelerating agencies applied to the movement of a boat.
Had Bridgman's Operational Theory been published at an earlier date, it is dubious that the present popular view of these electric and magnetic fields would be as they are. Why? Because the three electric and the three magnetic fields listed above are each one produced by operational means which are experimentally just about as different as they could possibly be. This fact alone should be sufficient to challenge complacency and initiate a searching investigation of the facts. Contrary to popular belief, each one of these fields is unique in nature. It is self-evident that each of these six fields requires unique operations necessary to produce, detect, and measure it. Both theoretical and experimental evidence will be presented to show that at least some of our conceptions of these fields are fundamentally misconceptions, and in these cases the misconceptions are due to the fact that these fields are unique in nature, each one possessing characteristic properties of is own which entitle it to a distinct identity in nature. This discovery must inevitably render a great service in clarifying the confusion existent in the present state of our knowledge, and afford new opportunities for research, new possibilities in applied physics and new horizons for a unified field theory. An analysis of the properties of these fields will next be considered so that their unique properties may be apparent.
Table 1 has been prepared to show the outstanding differences in the properties of each of the first three operationally different electric fields. The recognition of the uniqueness of each field is aided by a comparative study of these properties. The properties of the electrostatic field are well known and need no elaboration in this treatise. Scientific literature dealing with this field is replete with its well-known characteristics.
Table 1: Field Properties
Field Properties: (1) Spatially distributed energy; (2) ŘE
= ds ; (3) Curl E ; (4) ?ab E =
ds ; (5) E
=dV/ds Potential function ; (6) Behavior with respect to
shielding; (7) Div. E ; (8) Poisson's fundamental law with
respect to the interior of conductors; (9) In conductors
carrying current; (10) Inverse square law; (11) Spatial nature
of field; (12) Relation to charges in it; (13) Field dependence;
(14) Functional dependence on velocity.
; (5) E
=dV/ds Potential function ; (6) Behavior with respect to
shielding; (7) Div. E ; (8) Poisson's fundamental law with
respect to the interior of conductors; (9) In conductors
carrying current; (10) Inverse square law; (11) Spatial nature
of field; (12) Relation to charges in it; (13) Field dependence;
(14) Functional dependence on velocity.
Electrostatic Field: Es ~ (1) KE2/8 pi ergs/cc; (2) = 0 always; (3) = 0 always; (4) a constant always; (5) Yes; (6) Can be readily shielded with conducting material; (7) = 4 pi p; (8) Obeyed; (9) Conductors always have a surface charge; (10) Yes; (11) Continuous throughout space it occupies; (12) Charges within it produce a distortion of the field; (13) A primary field independent of all other fields; (14) Intensity of electrostatic field in any reference frame is parabolic function of v/c.
The electric field induced by a changing magnetic vector
potential: Et = -dA/dt ~ (1) KE2/8 pi ergs/cc ;
(2) / 0 in general; (3) = -dB/dt; (4) Not a
constant. Dependent on the path of integration; (5) No; (6) Can
be shielded with sufficient thickness of shielding; (7) = 0
always; (8) Not obeyed; (9) Can drive a current without a
potential drop along the wire; (10) No; (11) Continuous
throughout space it occupies; (12) Charges within it do not
distort the field; (13) Dependent upon another field; (14) ---.
The motionally induced electric field: Em = V
x B ~ (1) No spatially distributed energy; (2) /
0 in general; (3) = v x (v x B) / 0 in
general; (4) In a perfectly uniform B the value of the integral
between 2 points a and b will not be dependent
on the path, will be independent of it, but in general this will
not be true; (5) May or may not be a potential function; (6)
Immune to shielding; (7) = 0 always; (8) Not obeyed; (9) Can
drive a current without a potential drop along the wire; (10) By
special design yes in certain portions of field; (11) Only
present at points where moving charges exist; (12) Charges
within it do not distort the field at all; (13) Dependent upon
another field; (14) Intensity of motional electric field in any
reference frame is linear function of v/c.
In order that the unique character of each of the electromagnetically induced fields may be understood, considerable discussion will be required in view of the fact that so many texts emphasize the similarity of these fields in certain instances and fail to point out the vital, outstanding differences in their fundamental properties, which make it impossible for them to be identical in nature. Some of these differences have been revealed in scientific literature (16 ~ G. I. Cohn: Electrical Engineering 63: 441, 1949; E. G. Cullwick: The Fundamentals of Electromagnetism, pp. 84-87, Macmillan Co., 1939; W.V. Houston: American Physics Teacher 7: 373, 1939; Page & Adams: American Physics Teacher 3: 57, 1935)) but do not as yet seem to be generally incorporated in our textbooks. Cohn, in particular, has rendered an outstanding contribution…
[missing text?]
different ways of expressing one and the same fundamental phenomenon is because it is basically incorrect. Not only are the two types of field Em and Et fundamentally different and each one unique in nature, but an examination of the Faraday Lay, E.M.F. = -dN/dt, reveals that this equation itself does not hold true in general. In other words, it has been shown that the flux linking with a closed circuit can be either partially or completely removed from the circuit without inducing any electromotive force whatsoever! 17 ~ G. I. Cohn: Paradoxes of Electromagnetic Induction; Thesis, Illinois Inst. of Technology Library)
This can be accomplished by a cleverly designed switching circuit, one version of which is shown in Figure 1. This illustrates the fact that the flux linking with a closed circuit may be changed by three different unique operations: (1) Flux cutting, (2) Flux linking caused by -dB/dt, where the source of B is intrinsically changed with time, and (3) A uniquely designed switching circuit. Only the first two sets of operations produces an emf. The third set of operations produces no emf and for this reason the present manner of presenting Faraday's Law is invalid. There are two unique operational methods of inducing an emf, and we should not endeavor to derive them from one simple mathematical expression -dN/dt, because this expression includes or implies operations which will not induce and emf. It is therefore obsolete! As Cohn and others have shown, there are actually two kinds of electromagnetic induction and in general case both types are involved and each must clearly be understood and differentiated from the other. That the flux linking law, attributed to Faraday, does not hold for his own Faraday-disk unipolar generator, which requires the flux cutting law for its correct descriptive behavior, is perhaps one of the most outstanding examples of how vitally unique and essential is the role of each law and each of the corresponding electric fields produced by these laws.
Figure 1

In the Faraday generator there is no time rate of change in the magnetic induction B, since it originates from a permanent magnet and is constant. The circuit can even be made so as to link with no flux whatsoever. In any case, there is no change of B with time. This very fact that all contemporary authorities (18 ~ Slater & Frank: Electromagnetism, p. 86, McGraw-Hill, 1947) on this subject have found it necessary to add the flux cutting law to the famous Maxwell equations in order to satisfactorily explain all cases of electromagnetic induction is itself indicative of the uniqueness of the electric field so produced.
Many of my colleagues have said that it was not difficult for them to distinguish fundamental differences in the Coulomb field Ec and the magnetically induced fields Et and Em, but they were unable to see any clearly defined difference between the Et and the Em field. Let us, therefore, discuss some of the most outstanding differences between these two fields.
What is our concept of an electric field? Most physicists will reply that it is a force which acts upon an electric charge and tends to accelerate it in a definite direction termed the direction of the field. With this concept in mind, let us analyze the two electric fields Et and Em.
In Figure 2 below is shown a cross-section of a long straight solenoid in which a gradually increasing current is flowing counterclockwise.
Figure 2

The uniformly distributed magnetic flux density B within this
area is therefore increasing with time and according to
Faraday's law of Electromagnetic Induction, the emf around any
closed circuit placed wholly within the area shown in Figure 2
would be given by: emf = dN/dt = ?QEt-ds where N
equals the total flux linking the circuit.
![]()
Our interest centers on Et, the electric field within
the conductor of such a circuit, giving rise to the emf.
Obviously, Faraday's Law gives us absolutely no information
about this field Et other than to say that the line integral of
this field around the closed circuit will give us a value of the
emf induced in it. If this closed circuit A lies in the plane of
the area, Figure 2, then at point P in this circuit, it is
obvious that Et is directed toward the bottom of the
paper. If, however, we select the circuit B instead of A, then
at this same point P the electric field Et is
directed horizontally to the right. If we select circuit C
instead of B, we then find Et directed toward the top
of the paper at P exactly the opposite direction from that in
circuit A. And if we select circuit D then Et at P is
directed horizontally to the left, in exactly the opposite
direction that it had in circuit B. That an electric field Et
exists in this area there seems to be no doubt since an emf
arises within each of these circuits. But this field Et
is very peculiar, since it is impossible to define it at the
point P unless we first select a particular circuit through P
which will then enable us to determine its direction at P.
Now let us remove the conducting circuits from within the area of Figure 2, and place a stationary free charged particle Q at the point P. Will it move? If so, in what direction will it move? If it remains stationary, and is free to move, then does an electric field exist at this point? Certainly the magnetic flux density exists there and is changing with time, but we have no assurance whatsoever that it will act upon a stationary charge, nor is the direction in which it will act unless it is first given an initial velocity, or unless it is confined within the conducting medium of a closed circuit. No other electric field has this unique operational prerequisite, which in this case appears to require that the charged particle upon which it acts must either have an initial velocity within the electric field, or that it must exist within a conducting circuit before it will make itself manifest. A free stationary charged particle placed within an Em or Ec field will be immediately acted upon in both magnitude and definite direction. About all that we can say in a descriptive manner of Et at a point P, such as shown in Figure 2, is that this transformer type field has curl at that point, as shown by Maxwell's formula. For a clarifying conception of just what curl means one will find it helpful to study Skilling's treatment of it where he defines it as the limiting value of circulation per unit area (19 ~ H. H. Skilling: Fundamentals of Electric Waves, 2nd Ed., p. 41; J. Wiley & Sons, Inc, 1948). This means simply, as applied to Figure 2, that if a small conducting disk of ink, say a dot made with India ink, were placed at point P, negative electrons would circulate in this dot in a counterclockwise direction. The dot of ink would be everywhere at the same potential, and therefore uncharged. Curl is one of the most outstanding characteristics of the Et field which may or may not be possessed by the Em field, but never by Ec. Now place this same dot of India ink in a uniform Em field and it will become an electric dipole. The action of a uniform Et field on this dot is therefore very much different from that of an Em uniform field.
With the exception of mason and Weaver's text, little literature appears to exist which directs attention to the ambiguous nature of the concept of the spatial distribution of energy as concerns the two electromagnetically induced electric fields. That the electric field induced by a magnetic flux intensity which is changing with time has a spatial distribution of energy, whereas the motionally induce electric field does not have any such identical distribution of electric field in space is one of the most crucial of the fundamental differences in their properties. Since the establishment of this fact that these two fields differ radically in their relation to field energy is all-important to the objectives of this treatise, let us now take up a digression at this point.
Insofar as this writer is informed, no one questions the actuality of the special distribution of energy in the case of the electrostatic field or the Et field, due to a magnetic vector potential intensity varying with time (20 ~ The transformer law is usually stated in terms of the negative time ration of change of magnetic flux linking with the circuit and this gives the total induced emf. The electric field produced by this type of induction is most conveniently designated by the time rate of change of the magnetic vector potential.). Calculations involving field energy in the electrostatic case have long been made without difficulty, and the transfer of energy between the primary and secondary coils of a transformer without any movement of its component parts give direct evidence that electric energy is distributed in the space occupied by the Et field. The very nature of this electric field requires the concept of the spatial distribution of field energy.
An analysis of the nature of the motional electric field will reveal, on the other hand, that this concept of spatially distributed electric field energy, is not only required for a satisfying understanding of phenomena where this field is involved, but it actually induces basic ambiguities and impossible conceptions.
Let us now examine the origin and basic nature of the motional electric field with its unusual property.
Em = V x B. This vector field equation was derived by Lorentz from the empirical force formula of Biot and Savart. This is the electric field which is present in the moving wires constituting the armature coils of an electric generator. It causes an emf to exist in a conductor by virtue of motion across magnetic flux. Such induction is called a motionally induced emf or flux cutting emf. As we shall see, this field has some of the most unusual and interesting properties conceivable. Page and Adams have emphasized one of these unique properties. They point out in the case of the generator with a rotating armature coil that this field, "exists only in the moving conductor" --- where moving electric charges are present --- "since no electric field is present in the observer's reference frame" (21 ~ Page & Adams, op. cit., p. 16). Let us examine this aspect of the field more closely, for neither the electrostatic field nor the Et field possesses this property, for these fields can exist in an observer's reference frame, whether a conducting circuit, or conductor, or charge is at hand or not.
Three essential operational ingredients are necessary to bring this Em field into existence: (1) A constant magnetic induction B, (2) an electrically charged particle e (22 ~ the charged particle may be an electron in a piece of matter, or free as in a gas), a relative velocity v between the particle and the reference frame of the magnetic source producing B. A deflecting force will act upon the particle wherever it moves across magnetic flux lines. As viewed from the reference frame of the particle, this force (v x B) has many aspects of a real electric field and in fact it is termed a motionally induced electric field having an intensity (v x B) per unit charge. In the reference frame of the magnetic source giving rise to B only a magnetic field is present. One observes that the moving charge is acted upon by a force which to all appearances is wholly magnetic in nature. Whether we think of it as a deflecting magnetic force or an electric field, it is obvious that it exists only at the points in space where moving charges, either free or in matter, are present, for stationary electric charges are unaffected. In a vacuum, or in space between moving electric charges, no Em field or deflecting magnetic force exists. Hence it must necessarily have a spotty, or discontinuous nature. How can this be possible?
Let us proceed as Mason and Weaver have suggested by considering "a quantitative description of the individual behavior of charges". Let a positively charged particle with mass m and charge e be projected into a vacuum chamber with uniform velocity vo at right angles to the direction of uniform magnetic flux B. The particle has initial kinetic energy T = 1/2 m vo2. By Ampere's Law, the moving particle (or current element) is surrounded by a concentric distribution of magnetic flux.
Figure 3

It will be acted upon by a mechanical deflecting force F = e vo x B.
It will also be readily seen that this force on the charged particle exists only when there is a magnetic field about the particle. The force is actually the force of lateral repulsion between two magnetic fields. Without the presence of both magnetic fields, no such force exists, hence the existence of f requires the simultaneous presence of all three of its essential components, e, v and B. The actual action on the charged particle is magnetic in character, rather than electrical.
Let us next observe that the force f always acts at right angles to both v and B. Since the displacement of the particle is always in a direction at right angles to the force, this force can do no work on the charged particle upon which it acts, and no energy is extracted from B. This force, arising from the magnetic repulsion between two magnetic fields, one due to the moving particle, and the other due to the applied B, acts like a circular deflecting constraint or baffle, which only changes the direction but not the magnitude of the velocity of the particle. The speed of the particle and hence its kinetic energy remain unchanged. It is well known that such force will cause the particle to travel in a circular path, the radius of which is readily obtained by equating the force Bevo to the centrifugal force mvo2/r and solving for r, r = mvo/eB. The particle is thus trapped by the magnetic field, which will hold it to a circular path until its original kinetic energy is dissipated by collisions with neighboring particles, or by radiation.
It is of particular importance to this discussion and is again repeated, that since the deflecting force is always at right angles to the relative velocity vo of the particle and also to B, no work is done on the particle by the deflecting force.
Whether the particle is confined within the boundaries of a wire or not, (v x B) will always be at right angles to v and B. For clarification let us suppose the particle is enclosed within a frictionless tube the axis of which is at right angles to vo and to B. Few further impose the condition the velocity vo of the tube be kept constant in magnitude and direction. Let us examine the behavior of the particle within it. As the tube moves forward, the particle is prevented from moving in a circular path by the walls of the tube, but it can and will begin to move along the axis of the tube under the deflecting action of the magnetic field. To maintain the original forward component of its velocity vo constant, the external agency moving the tube will have to supply the particle with additional kinetic force in this direction.
As the particle acquires a velocity component vt along the axis of the tube, the resultant force v x B acquires two components, one along the tube, which will be constant (vo x B), and one at right angles to the tube (vt x B), opposing to the forward motion (Lenz's Law). We thus see the that the additional kinetic energy imparted to the charged particle moving down the tube is transmitted to the particle directly by the external force moving the tube. This kinetic energy is continuously channeled along the tube by the deflecting action of the magnetic induction B interacting with the magnetic field formed around the moving charged particle and the constraint of the tube itself.
The modus operandi of v x B is thus seen to be wholly magnetic in character. The conception of this force, when viewed from the standpoint of an observer at rest in the reference frame which is traveling with velocity vo, as being an electric field similar in character to that of an electrostatic field is therefore an artificial figment of the imagination which instead of clarifying the understanding of motional electromagnetic induction, often befogs it. The concept of v x B as an electric field is a convenient mathematical construct, however, for computing induced emf's, but the actual nature of the phenomenon with which one is dealing must be kept clearly in mind to avoid mistakes. The electromotive force induced between the terminals of a short straight linear conductor of length l moving with relative velocity across a magnetic induction B is given by the formula:
(Eq. 2) E = v x B • l
whereas that induced in a closed circuit is given by:
(Eq. 3) E = ? v x B • dl
![]()
and is often difficult to evaluate. In these formulae the term v x B represents the direction and magnitude of the fictitious electric field intensity em. The energy associated with this field is directly imparted to the charged particles by a mechanical prime mover which produces the relative velocity instead of by an actual electric field.
An important point in the foregoing analysis is that it serves to illustrate the fact that since the Em field is by its intrinsic nature only the repulsive force between two magnetic sources, that of B and that of the moving charge, it cannot exist except a those points where electric charges with magnetic fields about them exist. The Em field is only at those points where a magnetic field exists that can interact repulsively with the magnetic induction B.
Therefore, it is evident that there can be no continuous spatial distribution of Em electric field energy as there is in the case of the Eo or Et fields. Since no electric Em field exists in a space without charges, there is no Em field energy in a vacuum or in free space such as can exist with an electrostatic field. We need to remember this fact when we think of the Em field phenomenon from the viewpoint of a moving magnetic flux acting on a stationary electric charge. A single phenomenon when viewed from two different reference frames can appear to be fundamentally different, but such relative viewing does not alter the fundamental basic cause giving rise to it. Since the real basic nature of the v x B phenomenon has not hitherto been exposed in detail and hence is to a large extent currently taught and believed to be of an electrostatic nature by theoretical physicists, it will be worth our while to go into some of the subtle aspects it presents when it is so conceived.
Let us consider the popular view of this phenomenon as presented by most interpreters of relativity theory. The Special Theory of Relativity as applied to electrodynamics states that if we have a uniform electric field of intensity E, due to charges, and a uniform magnetic induction B, due to magnets, both at rest in a reference frame S, then in frame S' moving with uniform velocity v with respect to S an observer will find an electric intensity E', and a magnetic induction B' given in vector notation in absolute gaussian (c.g.s.) units by:
(Eq. 4) E' = ? {E - (1/c) v x B}
(Eq. 5) B' = ? {B - (1/c) v x E}
where ? = 1/? 1 - (v/c)2

and
c = 3 x 1010 cm/sec.
The current confusion among physicists is that many interpret
relativity theory as showing that ? v x B/c ![]() is an electric
field, identical in nature to an electrostatic field. The reader
will note that E' is the vector sum of two electric
intensities, ?E
is an electric
field, identical in nature to an electrostatic field. The reader
will note that E' is the vector sum of two electric
intensities, ?E ![]() , which is an electrostatic field, and V(v x B)/c.
Added in this manner, many physicists have tacitly assumed that
E' and ?v x B/c
, which is an electrostatic field, and V(v x B)/c.
Added in this manner, many physicists have tacitly assumed that
E' and ?v x B/c ![]() must likewise be interpreted as
electrostatic in nature. Jeans, however, points out that nothing
in the postulates of the Special Theory require such an
interpretation. He states, "the equations may be taken merely as
an expressing relations between quantities as measured by one
observer S and another S' moving at velocity v relative to S"
(23 ~ J. H. Jeans: The Mathematical theory of Electricity
& Magnetism, p. 606, Cambridge Univ. Press, 1923).
Cullwick states, "R is an attribute of the relativity equations,
that they do not claim to include any physical interpretation of
the phenomena" (24 ~ Cullwick, op cit., p. 119). Smythe states
that the forces represented by the added terms "differ from
electrostatic forces. One might call these additional forces
electrokinetic forces, but as we shall see, they are identical
with those we have already called magnetic forces" (25 ~ William
R. Smythe: Static & Dynamic Electricity, p. 488;
McGraw Hill Book Co., 1939).
must likewise be interpreted as
electrostatic in nature. Jeans, however, points out that nothing
in the postulates of the Special Theory require such an
interpretation. He states, "the equations may be taken merely as
an expressing relations between quantities as measured by one
observer S and another S' moving at velocity v relative to S"
(23 ~ J. H. Jeans: The Mathematical theory of Electricity
& Magnetism, p. 606, Cambridge Univ. Press, 1923).
Cullwick states, "R is an attribute of the relativity equations,
that they do not claim to include any physical interpretation of
the phenomena" (24 ~ Cullwick, op cit., p. 119). Smythe states
that the forces represented by the added terms "differ from
electrostatic forces. One might call these additional forces
electrokinetic forces, but as we shall see, they are identical
with those we have already called magnetic forces" (25 ~ William
R. Smythe: Static & Dynamic Electricity, p. 488;
McGraw Hill Book Co., 1939).
Winch in his excellent treatise states, "Notice that (v x B) is not an electrostatic field intensity for it is not due to a distribution of charges. We have shown that the line integral of electrostatic field intensity around any closed path is always zero and there is no exception in this case, i.e., the electrostatic field intensity set up by the displaced charges integrates to zero around any closed path. (v x B) is due to the motion of the conductor in the magnetic field, and an external agency is feeding energy into the system, and a net amount of work is done by a charge in moving completely around the circuit. Notice also the (v x B) does not exist in the absence of moving charges, because it is the magnetic force on the charges moving with the wire which sets up the electric field intensity" (25 ~ Ralph P. Winch: Electricity & Magnetism, p. 536; Prentice & Hall, Inc., 1955).
Notwithstanding such pronouncements, the writer has discussed the subject with many exponents of relativity theory who are quite insistent that all the terms in Equation (4) must be considered identical to, and indistinguishable from, an electrostatic field. A personal letter from a colleague at our National Bureau of Standards also takes this position, as well a several Nobel Laureates with whom he has consulted. And this stand is taken admittedly by these physicists without a single iota of direct experimental evidence with which to support it!
During the early stages of the work on this project, I called on several Nobel Laureates to discuss the worthwhileness of this endeavor, one of whom was the distinguished physicist and authority in the field of electrodynamics, Enrico Fermi, who had delivered a lecture at the 1944 Public Affairs Conference at Principia College. Among the questions asked, two will be of interest to the reader. (1) "If it were ever discovered that the motional electric field v x B/c was unique and not identical to, and indistinguishable from, an electrostatic field, would this discovery be of any great value to our scientific knowledge?" His answer in substance was: It would indeed be of very great significance and consequence. (2) "To your knowledge, do you know of the existence of any direct experimental evidence which confirms the belief that the motional electric field and the electrostatic field are identical in nature?" After considerable thought, his reply was, "Come to think of it, I can recall of no such existent evidence."
It will now be shown that the relativity equations themselves provide a means for obtaining a fuller understanding of the physical nature of the terms they contain. It is important to observe mathematically that in the general case every term of both of these equations (4) and (5) is a function of B where B = v/c. By a binomial expansion it can be readily shown that:
(Eq. 6) ? = [l + (l/2) ?2 + (3/?) ?4 + …]
![]()
Substitution in the two right hand terms of Equation (4) yields
(Eq. 7) Es = ? = [l + (l/2) B2] E
(Eq. 8) E'm = ? [v x B/c] = [l + (l/2) B2] (v x B/c) = BBn

where v and B are taken at right angles to each other and n is a unit vector at right angles to both v and B and terms of higher degrees that B2 have been dropped.
Equations (7) and (8) represent respectively the electrostatic, and the motional electric, field components of the resultant electric intensity E' in the reference frame S' moving with uniform velocity v with respect to S. If now E and B in reference frame S are adjusted so that they are both perpendicular to v and to each other and their intensities fixed at constant values such that:
E's -E'm = 0
Then these two electric field intensities will be equal in magnitude and opposite in direction (27 ~ Two large, similar, rectangular, parallel, and vertical plates separated by a distance d could be oppositely charged and electrically isolated in s. Above and below the air space between the condenser plates two large circular horizontal Helmholtz coils could next be fastened so that when connected in series a constant current through them would produce a uniform vertical magnetic induction B in the space between the condenser plates. Let S' be a frame of reference moving horizontally through this space with velocity v at right angles to both E and B.)
A stationary electron in S' will therefore experience no force acting upon it because the resultant electric intensity in this frame is zero. Most relativists claim that under this situation there will be complete cancellation of electric fields. It will be observed that E's and E'm are parabolic and linear functions of B respectively. It will at once be evident that although E's and E'm can be made equal to each other in magnitude and opposite in direction for any one reference frame S', moving with an assigned value of v and a fixed proper adjustment of E and B in frame S, such that v = cE/B, nevertheless such equality of E's and E'm would be possible for only two frames at the most, for a straight line can cut a parabola in not more than two points. It is thus self-evident that in the general case it would not be possible to make these two oppositely directed fields continuously equal in more than two possible reference frames at the most, by assigning fixed values to E and B in S. This is a clear-cut case of the simple superposition of two distinct types of fields. If the E'm term represented an electric field which is identical to and indistinguishable from an electrostatic field, then it would have to behave like one, which would require that it vary parabolically with ? instead of linearly. How could there be complete cancellation of fields in a particular frame if there is a real difference in their intensities manifest in the reference frames having both greater and lesser velocities than this particular frame? Surely such a situation calls for fields which are distinct and unique, balanced against each other with a zero resultant in one (or possibly two) particular frames, but not in neighboring frames of reference.
The (v x B)/c term most clearly simulates the characteristics of an electrostatic field when it is isolated by itself, without the presence of a resultant magnetic induction! It is this case which has been mostly responsible for the popular belief that the two fields are identical in nature. To simplify the picture, let us first assume a vertical uniform magnetic induction B in frame S and no electrostatic field present. In the reference frame S', moving with uniform horizontal velocity v, with respect to S, an observer will discover a horizontal electrical field, (v x B)/c and a vertical magnetic induction B' = B (assuming velocities small with respect to c), the path of a free electrified particle in frame S' under the action of the two fields which are at right angles to each other will be that of a cycloid traced on a horizontal plane. The path of the particle as seen in frame S would be circular, as previously shown. This motion projected on frame S' moving with velocity v, is that of a point on the circumference of a circle rolling in a horizontal plane along a line in the direction of -v. If we now superimpose a uniform magnetic induction B" equal in magnitude and opposite in direction to B', in frame S', then in this frame we will have only the isolated electric field v x B/c, with the resultant vertical magnetic induction of zero intensity. Now this electric field very greatly simulates that of an electrostatic field, and it is readily understandable that many physicists have so interpreted it. The path of the particle in this field is now rectilinearly in the direction of v x B/c in S', and parabolic as seen from S. Furthermore, since the curl and divergence of v x B/c in S' are both zero, as they are in the case of a uniform electrostatic field, mathematicians can call upon what is known as the identity theorem as a proof that the Em field is identical to an indistinguishable from an electrostatic field. This proof amounts to nothing more than saying that the dynamic behavior of a charged particle will be the same in both fields. In the following chapters we will show experimentally that this is not always true. Also analysis shows that a prime mover is required for moving the source of B" and supplies energy to the particle continuously.
Let us again analyze this case carefully because of its great importance. Kinetic energy is imparted to a free charged particle and gives it a velocity vo with respect to frame S. At the commencement of its motion the particle is at rest in frame S', which is moving with the same velocity. It appears to an observer in this frame that the particle starts from rest and begins to move in the direction of (vo x B)/c. If the magnetic induction is S' is only that due to B, then its motion v' with respect to S' will produce a new deflecting intensity v' x B'/c in frame S' in the direction of -vo. If, however, the equal and opposite magnetic induction B" is introduced in this frame, the effect would be to produce another deflecting intensity v' x B'/c which would be equal and opposite in direction to the intensity v' x B"/c. At this point one needs to think carefully. The deflecting intensity v x B'/c in S' directed against the forward motion of the particle arises by virtue of Lenz's Law. The force on the particle due to this intensity will act continuously as long as the particle moves at right angles to vo. To enable the particle to maintain constantly it original forward velocity vo, the kinetic energy which is being channeled at right angles to vo must be continuously replaced. To do this, work must be done continuously upon the magnet giving rise to B" in S', because the action of B" on the particle is to assist its forward motion with respect to S in exactly the same amount that v x B'/c depresses it. Two magnets are involved in this action. (1) The magnet giving rise to B' in S' and which is at rest in S. (2) The magnet giving rise to B" in S' and which must be continuously supplied with energy from a prime mover.
The particle can thus be made to travel rectilinearly in S', in the direction of (vo x B)/c provided energy is continuously given to it via the role played by B". This is the situation which appears on first inspection to be exactly like an electrostatic field. A free electron originally at rest in S' will be accelerated rectilinearly in S' at right angles to vo. The electron is seemingly without contact with any material body, hence the electric field (vo x B)/c appears to be the only source of its steadily accumulating kinetic energy. The energy would appear to have come from a spatial distribution also as in the electrostatic case, since (vo x B)/c is the only electric field present in S', and the resultant magnetic induction is zero. This appearance is exceedingly deceptive and is the basis of this current false assumption with respect to the motional electric field. No prime mover is required in the electrostatic case! The energy in this case comes from the field itself.
In the first place, we must remember that an electric field of the type (v x B)/c cannot of itself impart energy to the electron because its line of action is always normal to the velocity of the electron with respect to S, and to the direction of B. We will remember in one of our previous discussions, that this deflecting intensity was shown to channel the kinetic energy of the particle down a tube without itself imparting energy. The function of the tube actuated by a prime mover was to continuously supply to the particle the energy to so channel and prevent the particle from taking up a circular path in S or a cycloidal path in S'. We now discover that the superposition of a magnetic induction B" in S' accomplishes the same thing that the tube did. But this accomplishment can only be achieved by feeding energy to the particle continuously in the forward direction as the tube did and this is done by a prime mover acting on the magnet giving rise to B".This magnetic induction B" interacts with the magnetic field around the charged particle so as to continuously push the particle in the forward direction vo, thus replacing continuously the kinetic energy channeled at right angles by (vo x B)/c and thus keeping the velocity of the particle in this forward direction constant, thereby making its path in S' one that is wholly at right angles to vo. A prime mover gives kinetic energy to a magnet, and its magnetic field pushes on the magnetic field around the particle, and thus does work continuously, which in frame S' appears as increasing kinetic energy of the rectilinear motion of the charged particle. No magnetic field energy is used up in this transfer of energy to the particle. The magnetic field of the magnet is a physical part of the magnet which pushes against the magnetic particle with exactly the same force that the tube did in our earlier description. It performs the same function as that of the tube. There is no real electric field involved in this picture except that around the charged particle, which when moving (by Ampere's Law) gives rise to the magnetic field around it. Thus the whole action of an isolated (v x B)/c field on a charged particle, instead of being electrostatic has a description which is essentially the direct transfer of mechanical kinetic energy from prime movers to the particle. No spatially distributed motional electric field energy enters the picture of this field. The uniform and relative motion of two magnets with equal and oppositely directed fields and the presence of an electric charge released with kinetic energy from its position of rest in the reference frame of one of the magnets produces a combination of pushing and deflecting magnetic forces which causes the particle to behave as though it were in an electrostatic field. This should not surprise us. What should surprise is that physicists should have assumed, without direct experimental evidence, that these combined magnetic forces could be identical to and indistinguishable from an electrostatic field. A monkey and a man are two distinctly different agencies (we hope)! They can, however, exert identical forces on one and the same object, and if oppositely directed hold the object in equilibrium. But surely no one will use such an argument as evidence that a monkey is a man, or that a man is a monkey! Such, however, appears to be the nature of some arguments that (v x B)/c is intrinsically electrostatic. Cajori states: "The unscientific physical speculations of Aristotle held the world bound within their grasp for two thousand years; the unfortunate corpuscular theory of Newton controlled scientific thought for over a century" (28 ~ Florian Cajori: A History of Physics, p. 101, Macmillan Co., 1922).
It has taken over a century to pierce the fog created by the assumption of one, and only one, electric field by Maxwell. This assumption having served him well in formulating his beautiful electromagnetic equations, nevertheless became a prejudice, and interfered, more or less, with clear-sighted judgment.
The Electromagnetic Force Equation
Three outstanding electric field intensities when added together vectorially, constitute what has been termed the electromagnetic force equations (in kms unts):
(Eq. 9) E = Ec + Em + Et = Cr/4?eor3 + (B x V) - ?A/?t (29 ~ Cullwick, op. cit., p. 287)

In their A New Electrodynamics, Moon and Spencer derive
a new formulation for this equation based entirely on the force
between two charged particle Q1 and Q2 (30
~ Moon & Spencer, op. cit., p. 369). These authors show that
all possible electric intensities can be exerted by charge Q1
and Q2 due to (a) constant Q1, no relative
motion, (b) constant Q1, uniform relative velocity,
and (c) constant Q1, accelerated motion, when added
become respectively:

(Eq. 10) E = Ec + Em + Et = F/Q2 = Q1r/4?eor3 + Dr Q1/4?eor2 (v/c)2 [1-3/2 cos2?] -aa Q1/4?eoc2r dv/dt
Note that the Coulomb intensity Ec is the same in (9) and (10). The motional intensity Em and the transformer intensity Et differ in form but represent in each of the two equations the same identical accelerating agencies. The outstanding difference between the two equations is that with (10), one can calculate electric intensities without having to entertain any field concepts, electric or magnetic! The authors claim considerable advantages for their formulation (10) over that of (9), and show five examples, each of which involves difficulties and incorrect answers if the classical Maxwell equations are employed indiscriminately, but which find correct answers in every instance with their formulation (10) (31 ~ P. Moon & D. E. Spencer: "On Electromagnetic Induction, J. Franklin Inst., vol. 260, p. 213, 1955). What they do not point out is that when the terms of (9) are applied in the same discriminating manner with respect to the operational aspects of the problems, as was (10), the ambiguities disappear and correct answers are forthcoming.
The Principle of Superposition as applied to fields, states that when several fields are superimposed on one another, each will act as though the others were absent. The simple addition of the separate terms in both (9) and (10), tacitly implies that this principle holds true in all cases. This tacit assumption in turn stems from the assumption that there is but one electric field, and each of the three terms being of this one nature, can be superimposed and added vectorially. If there was but one electric field in nature, then one would have to admit that the simple addition of these terms is scientifically correct. If, however, we have several unique electric fields in nature, each with its own unique physical properties, then the Principle of Superposition as applied to these fields is open to question. To illustrate this point, let us consider a case where we have only the two uniform Ec and Em fields present, superimposed so as to be equal in intensity, parallel, and oppositely directed. Equations (9) and (10) then reduce to:
(Eq. 11) E = Ec - Em = 0
It becomes obvious at once that if there is but one electric field in nature, then the resultant field is zero. If, however, each of these fields is unique, and a physical experiment can be so arranged as to permit only one to act, while the action of the other is restricted (due to their unique properties) then, in this case, the resultant field will not be zero as required by equation (11). If then we can arrange such a unique experiment which will pit these two agencies Ec and Em against each other equally, we will have a critical means whereby experiment alone, not assumption nor dogma, will give us a clear cut answer to the question of fields, and the application of the Principle of Superposition. It becomes obvious that nature alone can give us the answer to the questions we have raised. If in such an experiment the equation (11) is unambiguously not zero, i.e., if one field can be made to act alone, in the presence of the other, then this experiment will prove experimentally the spatial existence of unique electric fields, one of which is unique by virtue of electromagnetic properties not possessed by the other.
In the next chapter we will describe in detail experiments which answer the questions we have raised.
Experimental Confirmations by Electrostatic Shielding
In the first part of this chapter we will deal theoretically with the subject of shielding in order that the full significance of the experimental work to be described in the latter part may be transparent to the reader.
Among the properties of electric fields, there is no single one which more clearly characterizes the uniqueness of the electrostatic field, in contrast to the electromagnetically induced fields, than the singular behavior of this field with respect to shielding. In order that this phenomenon may be thoroughly understood, let us first review the electrostatic behavior and then contrast this with that of the other two electric fields. This behavior has been termed the fundamental law of electrostatics first stated by Poisson:
"The equilibrium distribution of the charges on conductors must be such that the force on any particle of electricity in the interior of a conductor, whether solid or hollow, is zero, since in a conductor electricity can move freely and the existence of a force on the particle will cause a flow of electricity. Thus, the equilibrium condition requires that all charge resides on the outside surfaces and that no charge or electric field whatsoever exist in the interior."
Physicists are well acquainted with the fact that the Et field, present in transformer coils, caused by a varying magnetic induction with time, does not obey this law at low frequencies, and only at high frequencies and with heavy shielding can this field even approach being effectively screened out. Since Poisson's law is a fundamental law, which applies to all electrostatic fields, it becomes evident at once that the Et electric field cannot and does not qualify as being electrostatic in character. This means that the Et electric field must be unique in nature. Although most physicists are willing to admit that this field, which arises from the growth or decay of a magnetic flux with time, is not electrostatic, nevertheless they cling tenaciously to the belief that there is only one electric field in nature (32 ~ Sleplan, op. cit.). Believing that the isolated motional electric field v x B/c has been shown mathematically to be electrostatic in character because teachers of relativity theory have taught this, it is not difficult to stretch the imagination a little further to include the Et field. We will, however, proceed to present direct experimental evidence which confirms the claim presented in this thesis that the isolated motional electric field is note and cannot be electrostatic in character. As we have seen, nevertheless, this field had deceptive aspects which cause it to resemble in many ways the electrostatic field.
In order that the case may be transparently understood, let us consider a very simple case of relative motion. Let us assume that we have an inertial system S which has only a uniform downward magnetostatic induction B, and no electrostatic field is present. In the inertial system S', which is moving with uniform horizontal velocity v with respect to S, the transformation equations (4) and (5) yield:
(Eq. 12) E' = ? (v x B)/c
(Eq. 13) B' = ? B
![]()
For convenience, let us think of the system S' as a completely closed rectangularly shaped coach, made of aluminum, traveling due North with velocity v. Let us think of B as the magnetic induction due to the earth's magnetic field (presumed vertical). The transformation equations (12) and (13) inform us that an observer riding in his car would find a vertical magnetostatic induction B', both inside and outside the car, which for ordinary speeds would be identical to B. This induction would be reduced to zero by building around and attached to the car a large Helmholtz coil which would produce within and throughout the car an equal but oppositely directed induction B". By doing so we isolate the electric field E' within the car. An observer would find outside the car a uniform electric field E', directed from East to West, given by (12). Within the car, however, we know from experience that an ordinary electric field intensity probe would register zero, or no resultant electric field intensity. According to most interpreters of the Special Theory of Relativity, this is exactly what should be expected, since they claim ?(v x B)/c is identical to, and indistinguishable from, an electrostatic field, and it must, therefore, behave similarly with respect to shielding. Hence, according to this view, the aluminum coach, being a good conductor, has produced within it in accordance with the fundamental law of electrostatics a surface redistribution of charge which brings about the complete cancellation of all electric field within the car so that no charge or electric field whatsoever exists inside the exterior bounding surface of the car.
An entirely logical and different conclusion may now be arrived at by reasoning based upon our known laws of electromagnetism. The car is moving across a magnetic induction B directed vertically downward. Therefore every free electron within the aluminum shield will experience a force due to the electromagnetically induced field ?(v x B)/c urging it toward the right hand side of the car. Under the influence of this field a redistribution of charge thus takes place until an electrostatic field Es directed horizontally across the inside of the car from the West wall to the East wall, equal in intensity and oppositely directed to the inducing field is established. When equilibrium is thus established, there will be within the car two oppositely directed coterminous electric fields, of types Ec and Em, in balance such as to produce a zero resultant electric intensity.
The question before us now is, which picture is correct? Can it be that Es and Em are actually identical in nature and complete cancellation within the car takes place? Experimental evidence must answer this question, and it does, clearly and decisively. Before presenting this answer, however, it will be of interest to note some of the comments made by physicists with respect to this question and the dense fog which has surrounded it. A colleague at the National Bureau of Standards, giving a view in harmony with most interpreters of relativity theory, has, in a letter, written with respect to the inside of the shield:
"If it is assumed that magnetic induction has a certain property not in conflict with anything observed experimentally, it follows that there are two electric fields which at every point are equal and opposite in direction. One of these fields results from electromagnetic induction and the other from electric charges.
"If it is assumed that magnetic induction has another property, not in conflict with anything observed experimentally, it follows that at no point is there an electric field and on no element of surface is there an electric charge. Therefore, any prediction not in accord with both of these assumptions should be considered as lacking an experimental basis.
Smythe, in commenting upon the problem of measuring ground speed in an aircraft by measuring the emf induced in a device by translation across the vertical component of the earth's magnetic field, states:
"The question arises as to whether the effect disappears if the apparatus is electrically shielded in the airplane. We know that the magnetic field will penetrate nonmagnetic metallic conductors, but we also know that the induced electromotive forces in the shields will set up electric fields tending to counteract the fields induced inside." (33 ~ William R. Smythe, Static & Dynamic Electricity, p. 500, McGraw-Hill, 1939)
Thus, S' finds his airplane in a transverse electric field, (v x B)/c. he cannot therefore use any metallic shields about his apparatus.
Here again we have the uncertain popular view among physicists as to whether Es and Em are in this case identically equivalent concepts which completely cancel each other. We will now show that this does not occur.
The Ironing Board Experiment ~ (34 ~ Egbert Jones & W. J. Hooper: Physics 401 Project, March 26, 1954, Principia College Library)
This crucial experiment was so named because the apparatus resembled somewhat an ironing board on wheels. The object of the experiment was to detect and measure the voltage induced in a test coil by the motional electric field Em while it was in a balanced and uncancelled state with an equal and oppositely directed electrostatic field Ec:
Figure 4: The Ironing Board Experiment

Three electrical circuits were employed, all lying in horizontal planes, parallel to a large laboratory lecture table. The test circuit consisted of a coil of 100 turns of #27 B&S gauge insulated copper wire wound in a groove on the 3/4" edge of a plywood form in the approximate shape of an ironing board 1' x 7' 4", as shown in the scale diagram Figure 4. The terminals of this coil were connected to a Leeds & Northrup Microvoltmeter which was mounted on the plywood form, which in turn was equipped with rubber-tire wheels so that it could be pulled at a uniform North-South velocity along the lecture table by an electric motor coupled to a reduction gar. The precise velocity was calculated with the use of a meter stick and an electric timer. Surrounding the forward end of the test coil, a second circuit was wound on a plywood extension consisting of a single strand of #16 B&S copper wire held at a constant two-inch distance from the test circuit, and carried a uniform direct current so adjusted that the magnetic flux B" surrounding it would exactly cancel out the vertical component B of the earth's magnetic field at the location of the test circuit. The third circuit was a largely accurately constructed Helmholtz coil so mounted in the laboratory and adjusted that the trailing end of the test circuit moved horizontally in the central region (between the two coils) in which the vertical component of the earth's field was completely cancelled. The entire test circuit including the microvoltmeter was electrostatically shielded. A very heavy coat of aquadag was applied over the test coil and the top and bottom of the supporting plywood frame. In addition, aluminum foil was wrapped around the forward semicircular part of the test coil, and finally put over the entire front portion of the apparatus. When moved uniformly along the table, the shielded wires of the test coil along the two sides of the frame move horizontally in the earth's magnetic meridian and therefore cannot cut any flux. The trailing edge of the test coil in the central region of the Helmholtz coil likewise can cut no flux. The forward end of the test coil alone cuts the vertical component of the earth's field, and is not at rest with respect to the canceling flux B" of the secondary circuit. The shield, with the exception of the portion within the Helmholtz coil, likewise cuts the vertical component of the earth's magnetic field. We now have a perfect set-up with which to test experimentally whether or not the uniform isolated motional electric field is equivalent and identical to the electrostatic field. The walls of the shield have induced in them an emf which drives electrons to the west side and leaves a positive charge on the east side of the shield. We know that these charges will build up until the electrostatic field caused by this separation of charge will be everywhere within the shield equal and opposite to the intensity of the motional electric field giving rise to it. If they are equivalent and identical in nature, they will completely cancel each other out and the leading wires of the test coil will be in a field-free space. If a voltage is induced in the test coil, it will be because these two fields do not cancel each other, because they are unique and different in their fundamental physical natures. Table II gives the results of 19 different velocities which were carefully measured:
Table II
Trial ~ Distance (cm) ~ Time (sec) ~ Velocity (cm/sec) ~ MicroV (observed) ~ MicroV (theory)
1 28.9 46.1 .626 10.5 10.3
2 20.0 28.2 .708 11.5 11.7
3 20.0 28.6 .699 11.5 11.5
4 20.0 31.3 .639 10.2 10.5
5 20.0 28.4 .704 11.2 11.6
6 20.0 30.1 .665 10.5 11.6
7 20.0 29.4 .680 11.0 10.9
8 20.0 29.0 .590 11.2 11.4
9 20.0 28.8 .698 11.3 11.5
10 20.0 31.1 .644 10.5 10.6
11 20.0 30.8 .651 10.5 10.7
12 20.0 30.7 .651 10.7 10.7
13 20.0 31.7 .632 10.7 10.4
14 20.0 32.1 .623 10.0 10.3
15 20.0 32.5 .615 10.2 10.2
16 20.0 32.5 .616 10.0 10.3
17 20.0 32.2 .623 10.1 10.3
18 20.0 32.0 .625 10.5 10.3
19 20.0 32.4 .618 10.0 10.2
202.1 204.5
Average Values: 10.64 10.76
v = nvBl (volts; n = 100; B = .55 x 10-4 Webers/m2; l = .30 meters
The experimental average value of induced voltage is lower than the calculated theoretical average value by only 1.11% and is well within the possible experimental error.
The argument has been advanced that this experiment proves nothing since by Faraday's law an emf is induced where there is a time rate of change in total flux linking the circuit, and this experiment involved such a time rate of change and, therefore, the results should have been expected, for it is known that shielding is not effective in transformer cases in which this law is applicable. This argument is not valid for the following reason. We have shown in Chapter 1 that the flux linking a closed circuit can be changed in only three possible ways: (1) flux cutting, (2) the growth and death of flux as in transformer phenomena, (3) special switching arrangements. Items (2) and (3) were obviously not involved in this experiment. Therefore there can be no appeal to transformer phenomena. The flux density B is constant throughout the experiment and therefore Maxwell's equation Curl E = ?B/?t, which is his interpretation of Faraday's Law, cannot be invoked. The experiment is so designed that the only possible seat of induced emf would have to be in the aluminum shielded leading wires of the test coil. The motional electric field alone is involved.
A brief account of two other shielding experiments carried out in the writer's laboratory to provide interesting qualitative demonstration equipment will now be described.
The Trapeze Experiment
The trapeze bar was made of six one-meter length pieces of soft iron pipe telescoped within the other. A single strand of insulated and electrostatically shielded wire was threaded through the innermost pipe of the bar and fastened at two places in the ceiling of the laboratory in such a manner as to permit the trapeze to swing horizontally in a North-South direction while the supporting wires on each side moved in the magnetic meridian and therefore could cut no magnetic flux. The shielded wire was connected to a sensitive wall galvanometer which was also shielded. Here again we have only the isolated motional electric field involved, for it is well known that the iron pipe would completely screen out the earth's magnetic field from the interior. With this simple apparatus, it ca be readily demonstrated that any small horizontal movement of the bar causes a deflection of the galvanometer directly proportional to its velocity. No measurable magnetic flux exists within the innermost pipe, but the electric field Vx B is present without diminution, and uncancelled by the equal and oppositely directed electrostatic field set up by the separation of charge in the shield. The wire in the pipe cut the vertical component of the earth's magnetic field, but was at rest with respect to the bar. The deflections of the wall galvanometer for a given speed were identical with or without the iron pipe and electrostatic shielding around the wire in the trapeze bar.
The Aluminum Box Experiment
In this experiment the entire apparatus was contained in a closed aluminum box which was moved horizontally in a North-South direction on a laboratory table. The test coil was rectangular in shape, made up of many turns of fine, flexible, insulated copper wire. The North and South sides of the rectangular coil were rigidized and supported in the same horizontal plane within the box. The South side was fastened to the inside South wall of the aluminum box and the terminals of the coil were connected to a sensitive portable galvanometer also mounted on this wall so that the pointer could be read through an opening in the box. The North side of the coil was supported in a fixed position by two plastic rods which were clamped to fixed vertical support rods on the table, and extended horizontally through holes in the aluminum box. The flexible East and West sides of the test coil hung in the magnetic meridian of the earth's field. Any movement North or South of the box thus caused these wires to either sag or become taut respectively. The presence of the uncancelled motional electric field can be demonstrated to be existent in the test coil when the box is completely closed and moved with various speed, North or South, across the earth's vertical magnetic field component. The deflections of the galvanometer with various speeds of the box are identical with those obtained when the shielded box is eliminated from the experiment and just the south side of the coils and the galvanometer were moved as before.
Summary
Let us make a brief summary of what we have thus far presented with respect to the motional electric field. Mathematical, operational, theoretical and experimental evidence convincingly confirm the concept of the motional electric field as physically real and distinctly unique. Its magnitude varies with reference frames in a manner unlike the electrostatic field. The crux of the theoretical argument involving this field amounted to the fact that the direct transfer of kinetic energy from a prime mover to a charged particle can be logically traced in detail and in accordance with known laws, and fully accounts for all energy transfer, whereas the conception of motional electric field energy existing at all and being distributed spatially, in addition to being capable of transfer, is next to impossible. The crucial evidence of uniqueness is experimental and it has been shown that this field does not obey Poisson's Fundamental Law of Electrostatics with respect to shielding. If the magnetic field has no physical reality, then when the motional electric field was balanced against an equal and opposite electrostatic field, the magnitude of the two terms in Equation (5) of the "New Electrodynamics" would have been identically equal and opposite and their algebraic sum equal to zero. The foregoing experimental evidence requires a concept of something real to account for the real difference experimentally measured. The magnetic field and the motional electric field concepts constitute that "something of fundamental physical significance" which was intentionally but ill-advisedly omitted in the new formulation in terms of particle electrodynamics.
Upon the foregoing evidence we rest our case that this motional field is unequivocally a unique electric field possessing its own nature, behavior and properties. We have asked nature a question and the reply is clear and unequivocal. Quantitative and qualitative experimental evidence such as has been carefully obtained in this case always has the last word. It closes the door on controversy and opens it wide toward the dawn of new horizons. Nature herself has given the answer which, in the words of Enrico Fermi, should "indeed be of great significance and consequence" to our scientific knowledge. The implications and consequences of this discovery will be discussed more fully later. They do, however, lead us immediately to the necessity for making inquiry into the basic nature of the analogous motional V x E/c magnetic field. This we will do in the next chapter.
The Motional Magnetic Field
The classical belief that nature has provide us with one and only one magnetic field has so befuddled reason that physicists have sought to eliminate the magnetic field concept entirely. To illustrate the ambiguity, the magnetic field arising from two operationally different sources will be described. The impossibility of these two fields beings identically the same becomes apparent upon comparison:
(1) The magnetic flux arising from the steady flow of electricity in a solenoid can be measured in intensity and in spatial energy content at any point in the surrounding space by an observer, either at rest or in motion with respect to the solenoid.
(2) The second source can best be described by a quotation from Sir Arthur Eddington:
"Consider an electrically charged body at rest on the earth. Since it is at rest, it gives an electric field, but no magnetic field. But for the nebular physicist it is a charged body moving at 1000 miles a second. A moving charge constitutes an electric current which in accordance with the laws of electrodynamics gives rise to a magnetic field. How can the same body both give and not give rise to a magnetic field? On the classical theory we would have to explain one of these results as an illusion. On the relativity theory, both results are accepted, magnetic fields are relative." (35 ~ A.S. Eddington: The Nature of the Physical World, p. 22, Macmillan Co., 1929)
The magnetic field arising from the solenoid is obviously born by the cooperative relative motion between unlike electric charges, such as the flow of negative electrons past the positively charged atoms in a copper wire. This type of magnetostatic field intensity is given the symbol Hs and is identified in Maxwell's equations by Curl Hs = J where J is the current density. B = mu Hs. Mu is the permeability (mks units).
![]()
The second type identify by the symbol Hm and arises wholly from relative motion v with respect to electric charges. This intensity Hm = V x Dc = EV x Ec (mks units) where E [Epsilon] is the permitivity, and Dc = EEc.
That the two magnetic fields Hs and Hm cannot possibly be identical in nature is proved mathematically as in the case of the Ec and the Em electric fields. The general mathematical expression for these two fields are obtained from the Einstein transformation equation (5) in free space where B = H in absolute gaussian (cgs) units as follows:
(Eq. 14) H's = B's = ?Hs
and
(Eq. 15) H'm = B'm = ?V x Ec
where ? = 1/?l - (v/c)2 and c = 3 x 1010 cm/sec.

Inspection shows that if the two magnetic fields H's
= ?Hs![]() and H'm = ?V x
Ec
and H'm = ?V x
Ec![]() were parallel and balanced against each other, for constant
values of Es and Ec, there
is one and only one possible value of v for which these two
fields would have the same numerical value. In other words, if
they were balanced against each other in one reference frame,
they would immediately be out of balance and could not possibly
cancel each other in any other frame of reference. Hence they
cannot possibly be the same kinds of magnetic field, because
they behave differently with change in reference frames.
were parallel and balanced against each other, for constant
values of Es and Ec, there
is one and only one possible value of v for which these two
fields would have the same numerical value. In other words, if
they were balanced against each other in one reference frame,
they would immediately be out of balance and could not possibly
cancel each other in any other frame of reference. Hence they
cannot possibly be the same kinds of magnetic field, because
they behave differently with change in reference frames.
Because Hm = V x Ec is a magnetic vector directed at right angles both to V and Ec, the electric field Ec can do no work, since any displacement of a magnetic particle will be a deflection at right angles to this field. The Hs magnetic field, however, can impart energy directly to a magnetic particle from its field energy.
The two types of magnetic fields described above have such
obvious dissimilarities that the only possibility of a
consistent satisfying picture of them is obtained by the
application of Bridgman's Operational Viewpoint. When this is
done we see these fields as unique. The first type Hs
is analogous to the Coulomb electrical field Ec
in that it has physical reality, and has a spatial distribution
of magnetic energy ?H2/8? ergs/cm3 ![]() . The motional
magnetic field Hm is analogous to the Em
field in that it too disappears when there is no relative
velocity.
. The motional
magnetic field Hm is analogous to the Em
field in that it too disappears when there is no relative
velocity.
The intimate relationship and unity between electricity and magnetism is seen in these two fields. The motional electric field can be described as a magnetic deflection phenomenon produced on moving charges, and the motional magnetic field can be viewed as an electric field deflection which will act on moving magnetic poles.
One of the thrills of this research project was predicted by Bridgman when he wrote, "In this self-conscious search for phenomena which increase the number of operationally independent concepts, we may expect to find a powerful systematic method directing the discovery of new and essentially important physical facts." (36 ~ ibid., p.224)
It is worth our while to note that we have six such unique field concepts shown on page 11 instead of the classical two, or the modern particle dynamics with none! These new field concepts when understood in connection with the equations of modern electrodynamics completely eliminate the paradoxes and ambiguities which have plagued this subject for years and explain electromagnetic induction which particle electrodynamics cannot handle. Most of all, they open up new horizons for the unification of the three great fields of electricity, magnetism and gravitation
Gravitation
"In the limited nature of the mathematically existent simple fields and the simple equations possible between them, lies the theorists' hope of grasping the real in all its depths." (37 ~ Albert Einstein: Essays in Science, p. 110; Philosophical Library, NY, 1934)
"It may well be that the approach of a new theory cannot begin until the mathematical nature of the old ones is clearly understood." (38 ~ Freeman J. Dyson: Scientific American, September 1958)
In the previous chapter we have shown how Bridgman's Operational Viewpoint applied to our "existent simple fields and the simple equations possible between them" has enabled us to gain an understanding of "the mathematical nature of the old" classical equations of electrodynamics which were beset with limitations, ambiguities, and paradoxes.
In order to obtain correct answers to our problems, it has been taught us that they must be analyzed operationally (40 ~ This becomes self-evident to anyone who will review the publications already cited, referring to Cohn, and to Moon and Spencer) to determine the particular types of fields that are involved, and the particular formulae among the six field types available must be selected and employed for the solution. The properties of each field type must be taken into consideration in working out problems. This clarified, straightforward procedure, working with unique field types, affords present possibilities that were not available to Einstein, due to mental doors which were closed.
It was without question Professor Einstein's life ambition to find the link between the gravitational field and the phenomena of electricity and magnetism. The reason for his failure appears now to be transparent in the light of this thesis. Most interpreters of his special theory, including Einstein himself, recognize the existence of but one electric field, in spite of the fact that Sir James Jeans has pointed out that such an interpretation of the terms in the transformation equation of his theory is not required by the postulates of the theory itself. (41 ~ J. H. Jeans: The Mathematical Theory of Electricity & Magnetism, p. 606, Cambridge Univ. Press, 1923)
In the English translation of his volume, Mein Weltbild, Einstein makes several very pertinent remarks which bear upon this thesis:
"It would of course be a great step forward if we succeeded in combining the gravitational field and the electromagnetic field into a single structure. Only so could the era in theoretical physics inaugurated by Faraday and Clerk Maxwell be brought to a satisfactory close." (42 ~ Albert Einstein: Essays in Science, p. 19; Philosophical Library, NY, 1934)
In this chapter we deal with one of the "simple fields" which has been known for years and universally employed in the generators of our electrical power plants, the unique nature of which has been unrecognized and its usefulness only partly exploited.
The greatest hurdle to be overcome in attempting to link gravitational force with any of the other known field forces of nature, is that property of gravity which enables it to act without apparent diminution in and throughout all kinds and combinations of matter. Insofar as we are aware there is no kind of matter which acts as an effective reflector or absorber of this force.
Let us now review the results of the experiments described in Chapter 3, the Ironing Board Experiment, the Trapeze Experiment, and the Aluminum Box Experiment. In all of these experiments the motional V x B suffered no diminution by virtue of the kinds of electrostatic shielding employed (i.e., iron, aluminum, brass, aquadag). We knew with certainty where the seat of action of the induced motional electric field was localized in these experiments. The behavior of this field in these experiments, therefore, has aspects which are exactly similar to gravity. Even when the resultant B itself is reduced to zero, VxB exists unaltered! No other force exists, to our knowledge, with such an unalterable and penetrating nature except that of gravity!
With the experimental evidence of the fact that the V x B field can in no instance be shielded from a region of space by a conducting shell and that it does not possess the properties of an electrostatic field, as has been tacitly assumed by theoretical physicists without experimental evidence to support it, we are brought face to face with the fact that this V x B field is really something entirely different than it has been hitherto thought to be, in spite of the fact that it is the generating field so active in our electrical power plants. Indeed it will be shown that this field should behave in a manner that is identical to gravity.
Let us remember that this VxB field is an electric field, that is, it will exert a force on, and will cause the acceleration of electric charges. In this respect it is similar to an electrostatic field. But an electrically neutral conductor places in a VxB field is acted upon differently than when it is places in an electrostatic field. In the latter field only an outside surface redistribution of charge and field take place whereas in a VxB field the neutral conductor experiences an internal redistribution of charge throughout its entire interior with two types of electric fields existent within the interior, balanced against each other in the equilibrium state. This state of affairs has been experimentally verified in the writer's laboratory and this evidence is the crucial blow which overthrows the popular view that the VxB field is electrostatic in nature. In the electrostatic case the field is entirely on the outside of the conductor, whereas in the VxB case, this field exists both within and without the conductor.
Within a conducting enclosure which is placed in an electrostatic field, this field is well known to be self-cancelled, whereas when placed in a motional electric field, this field gives rise to what has been thought to be a canceling electrostatic field equal in magnitude and oppositely directed, but contrary to popular belief this motional electric field is uncancelled by this induced electrostatic field and remains undiminished in intensity and in balance with it. This immunity to cancellation by shielding is the property which it has in common with gravity.
It is the penetrating property of the B x V field which qualifies it to play the role of a gravitational field (43 ~ The term B x V is use when one refers to a source which causes a magnetic flux B to move with a velocity V as would be the case when the field originates in atoms of matter. Mathematically, V x B = -B x V). This field can reach to every part of atomic structure and in and throughout the nucleus. Magnetic shielding cannot prevent it because B x V exists, regardless of the presence of a resultant B, which may or may not be zero. It seems incredible that this penetrating nature was discovered even in the days of Faraday and yet so little attention has been given to it.
In describing the work of Faraday on electromagnetic induction, Maxwell stated that the intensity of the induced electric field "is entirely independent of the nature of the substance of the conductor in which it acts" (44 ~ Clerk Maxwell: Electricity & Magnetism, vol. 11, p. 181). This was also later found to be true for dielectric substances as well as conductors.
Matter, as we know it, consists of electrons, protons and neutrons. The actual nature of the neutron is not known with certainty. This we do know, that a neutron does emit a beta particle, an electron. We also know that a proton can by electron capture turn into a neutron. While the present tendency is against the belief that the neutron consists of a proton and an electron in close bond, this thesis assumes that it does have an internal structure composed of opposite electrical charges. We so know that it has a magnetic moment. If magnetism is due to charges in motion, then we cannot be far wrong in this assumption. Electrons and protons also have magnetic moments. In other words, each of the elementary particles which make up ordinary matter has associated with it a magnetic moment, electric charge, or charges. In the experiments of Stern and Gerlach, magnetic moments were measured by causing a beam of particles to pass through a wedge-shaped magnetic field which deflected them.
Let us consider a solid cylindrical bar magnet of circular cross section rapidly rotated about its longitudinal axis. While it is well known that in this case the magnetic field does not rotate with the magnet, let us assume for convenience that it does rotate with the magnet. If the axis of this magnet is vertical with the North pole uppermost, then in the equatorial plane midway between the poles of the magnet we will have a magnetic field everywhere directed vertically downward, and the motion of this field will be toward the observer on one side and away from the observer on the other side of the magnet. In this equatorial plane there will also be a radial horizontal BxV electric field. This field will be convergent or divergent depending on the direction of rotation of the magnet.
Let us consider what would happen if an atom of any kind of matter is placed in a convergent or divergent BxV electric field. The planetary electrons will all experience a force which will shift their orbits slightly, say away from the axis, whereas the nucleus would be pulled toward it. There will be a very small differential in the magnitude of these two forces due to the slight shift in the position of the center of mass of the electrons with respect to the position of the nucleus. In this case, the push on the electrons will be less than the pull on the nucleus. The net effect of this will be a small attractive force which will tend to move the atom toward the axis of the magnet. Even a single neutron placed in a convergent BxV electric field might experience this attractive force if its constituents are oppositely charged attractive particles. Such a field might be employed to investigate the composition of the neutron! The crux of this paper is that it proposes that gravitational force is none other than the difference between the pull and the push of a convergent or divergent BxV electric field acting on the electrical constituents of atoms.
The consequences of this proposal would mean that the phenomenon of mass is independent of weight. An electron alone in such a field might be repelled while a proton would be attracted. This is a staggering thought, but we know of a certainty that an electron or a proton by itself actually has weight? Might not the negative charge which the earth is known to possess be due to a radical convergent BxV field emanating from the atoms composing the earth? If all neutral matter consists of equal numbers of oppositely charged electrical particles then the total mass of a body would be proportional to the total charge of one sign contained within it. It is here proposed that the earth's gravitational field might well be a convergent BxV field. We know that such a radial field is uniquely qualified to penetrate all space occupied by matter and produce a differential attractive force toward the earth's center of gravity by separating elementary charges of opposite sign only a trifle from their normal mean positions and thus making the pulling force on the positive charges slightly greater than the pushing force on the negative charges.
Each of the elementary particles of which all matter is composed is also an elementary magnet. The atom of today is a dynamic model. Each of these magnets has motion of some kind --- orbital, vibrational, precessional. In addition to possessing a magnetic moment due to spin, planetary electrons orbiting nuclei generate magnetic fields. These motions of the elementary magnets produce BxV fields which extend into space outside the atom. Nowhere in modern theory is an account given of these super-imposed BxV fields emanating from all matter. On might think that in ordinary nonmagnetic matter they would all cancel out since this is what happens with the magnetic fields in such matter. The electrons are paired in the various energy shells (of most atoms) in such a way as to effect this cancellation of magnetic fields outside the atom. Theory shows that if two such paired planetary electrons revolve in opposite directions, one clockwise and the other counter-clockwise, their magnetic fields due to spin at a point outside the atom can cancel each other out and that their BxV fields can constructively reinforce each other. The capital theoretical discovery, however, comes from a study of the magnetic field generated by the orbital motion of the planetary electrons. The negative electron, revolving about a positive nucleus, clockwise or counter-clockwise, gives rise to a BxV field which is, in either case, always directed radially inward toward the nucleus from points outside of atoms. The magnetic fields of two such oppositely revolving electrons will cancel, but the BxV fields reinforce each other. That these fields are directed radially inward makes it possible for them to account for the known drift of positive ions in the atmosphere down toward the earth and the opposite movement of negative ions upward. Because of its promising potentialities let us now take up an analysis of the magnetic field and motional electric field arising from orbiting planetary electrons.
Let us take for our model the simplest possible example, the Bohr Hydrogen Atom. Consider the nuclear proton at rest and the negative electron as revolving in a circular orbit of radius ro about it with angular velocity v. The Ampere-Biot-Savart expression for the magnetic field B generated about a charge q moving with velocity v is in mks units:
(Eq. 16) B = q v x r/r3
where r is the radius vector from q to a point P where B is measured. If the electronic charge -q is moving through free space without association with neighboring charges then we know that B appears as a motional magnetic field due to relative velocity of the electric field of the charge with respect to the observer at P. In this case, if the observer moves with the same velocity v as the charge, then the magnetic field at P disappears. On the other hand, if -q is moving in a linear conductor with relative velocity v, then an observer at the point P will observe a magnetic energy field B, whether or not he is stationary or moving. The actual value of B will of course be altered if the observer takes on relativistic velocities. But B will be observed in any frame of reference moving through, or stationary at, the point P. We now inquire with regard to the status of B at a point P when the planetary electron is revolving about the proton in a Bohr atom. Since we know this field is generated by cooperative action with the positive nucleus and that planetary electrons in magnets contribute components of orbital magnetic moment, we know that B must be an energy type magnetic field. The Ampere-Biot-Savant formula requires that at any instant the maximum values of B will be found at points along a rotating radius vector drawn from the proton through -q to the point. This means that the magnetic field energy of B is moving in a concentric orbit with the electron, with a tangential velocity V = (ro + r)w at any point a distance r from -q. If the magnetic field which the electron carries about it as it revolves in its orbit were of the motional magnetic field type Es x V generated solely by the relative motion of a single electric charge and an observer, then one could hardly impute motion to it. However, in this case we know the magnetic energy is itself a physical reality by virtue of its known type. This toroidal-like band of energy obviously holds a fixed relative position with respect to the orbiting electron, and hence moves with it.
This moving magnetic field, we know, will in turn give rise to a motional electric field B x V. This is illustrated in the accompanying Figure 5.
Figure 5

When the electron has a counter-clockwise motion in its orbit, it will give rise to a B at point P which will be directed up out of the page. V will have the same direction as v, and B x V will be directed radially inward toward the proton. We will call this a convergent motional electric field. Let us now calculate the value of this field at any point P on the radius vector from the nucleus through -q when the electron is the upper part of its orbit.
Em = B x V = -q(v x r) x V/r3
And when r >> ro, v = rw and v = row
(Eq. 17) Em = -qrow2/r approximately
We note that as the electron swings through the upper half of its orbit a motional electric pulse directed toward the nuclear proton with a maximum intensity varying inversely as the distance from the electron should be present at point P. As it continues to swing through the lower part of its orbit it is at this time not clear just what effect will be present at P. Our knowledge of the structure of the fundamental particles is so small that we cannot say whether or not the electric field about the proton itself will rotate about it as the electron revolves in its orbit. The electron is the particle in motion and there appears to be good reason to believe that the magnetic flux generated around it will be confined, on one side mostly between the electron and the proton, and on the other side of the electron out into space with its maximum intensity lying in the electron's equatorial plane at right angles to its orbital velocity. This is clearly not the equivalent of the effect due to a continuous current flowing in a conducting circular loop. In this latter case one would have a magnetic dipole at any instant in time, whereas in the case of a single electron we are dealing at each instant in time with circular loops of flux, without poles, with the electron located eccentrically within the circles.
Let us digress at this point and consider another phenomenon to which we should give some attention. An electron has spin, and is itself a small magnetic flux emanating from it. Out experimental knowledge regarding the behavior of magnetic fields with respect to rotation about axes of magnetic symmetry is such that we can state with considerable certainty that the magnetic field of the spinning electron should undergo a motion of translation only, as its axis revolves in the electron orbit. This means that at the point P in Figure 6, the magnetic flux due to the electron will partake simultaneously of two superimposed linear simple harmonic motions, one toward and away from the atomic nucleus and the other at right angles to this direction. As the magnetic flux moves across the point with these two motions, two component motional electric fields will be induced there. The motion of flux toward and away from the proton will induce an alternating electric field which will always be at right angles to the line d. The motion of flux at right angles to this line will likewise induce an alternating electric field which will always be directed along this line but will have a greater intensity in one direction than the other. The vector resultant of the motional electric field E at the point P will be a variable vector, rotating counter-clockwise with angular velocity v and it will trace out a pear-shaped figure with the major axis directed along the line d. The point P is near the top of the figure farthest removed from the atom.
Figure 6

E = B x V
W = dw/dt = angular velocity of B x V field in
volts/m.
E = Electric intensity of B x V field in
volts/m.
B = M/D3 Magnetic flux density due to M (in W/m2)
at P. It is directed down into the paper.
N = Proton nucleus.
M = Electron magnetic moment directed up out of the paper.
V = rw = Tangential velocity in m/sec.
It can be readily shown that the motional electric field intensity at P will be given by:
(Eq. 18) E = B x V = BVm = M/D3 rwm
where m is a unit vector parallel to r but oppositely directed.
Since D = ? r2 sin2 ? + (d - r cos ?)2
E = vMm / [r2 sin2 ? + (d-r cos ?)2]3/2
Since sin2 ? + cos2 ? = 1
E = Mrwm / [r2 d2 - 2 rd cos ?]3/2
And when ? = 0? E = Mrw/(d-r)3 toward the atom,
When ? = 180? E = Mrw/ (d-r)3
And when ? = 90? or 270?
E = Mrw/(d2 + r2)3/2
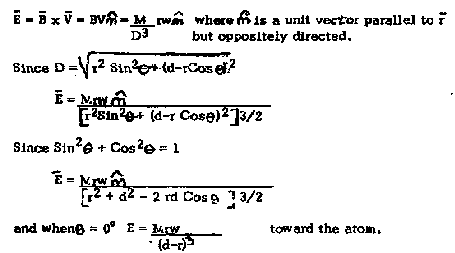

Graphed as a function of time, Ey along d would appear somewhat as shown below:
Figure 7

Whereas Ex would resemble a sine curve with equal positive and negative amplitudes.
Our analysis thus far has led us to two quite dissimilar motional electric field which should be found emanating from all matter. The first one we found arises from the rotary movement of the magnetic flux which forms around the planetary electrons in their orbital travel. The second arose by virtue of the translational motion of the magnetic flux of the spinning electrons as they revolve in their orbits. The first effect generates a radial electric intensity which varies inversely as the distance from the planetary electron. The second effect varies inversely as the cube of the distance. We shall now show that the first effect could very well be the agency giving rise to gravitational attraction, whereas the second effect would produce a very short range attractive field varying inversely as the fourth power of the distance, which obviously disqualifies it for the role of gravity, although it may prove to have some utility otherwise, as we shall see.
As stated earlier in this text, any material object placed in a convergent motional electric field should experience a force tending to move it into a more intense region of the field. When placed in the field, the body becomes electrically polarized and a very small separation of charge distribution should take place in every atom of the body. The charge nearest to the more intense region of the field will experience a pull which will be slightly greater than the push on the charge which is more remote, hence the resultant attractive force. Let us calculate this force in the case of the motional electric field generated by the electron as it orbits around the nucleus of an atom.
Returning to Figure 5, let us imagine that another hydrogen atom is placed at point P. Every time the electron swings around in its orbit at a frequency of 6.8 x 1015 rev/sec, the atom at P finds itself momentarily enveloped in a convergent B x V field. The positive nucleus will experience a pull toward the attracting atom while the electron will experience a push away from it. The field Em at the point P is given by equation (17). A charge Q placed in an electric field Em experiences a force F given by:
F = QEm
Differentiating this equation with respect to r in order to obtain the difference between the pull and the push, we have:
dF/dr = Q (dEm/dr)
Hence, if the difference dF causes a small separation dr of change in the mean distance between the proton and electron in the attracted atom, we have:
dF = Q(dEm/dr)dr
Differentiating (17) with respect to r, to obtain dEm/dr and inserting this in (19) and solving for ?F, which is the difference between the pull and the push, we have:
(Eq. 20) ?F = Qqrow2 ?F/r2
![]()
It is important to understand just what equation (20) represents. The motional electric field intensity Em given by equation (17) represents a radially convergent field. The intensity of the field decreases inversely as the distance r. When an H atom is placed in this field the positive proton is attracted toward the source of the field while the electron is repelled. If a separation of the center of charges takes place (polarization), i.e., if the proton moves slightly toward the source and the center of the deformed, somewhat elliptical, electron orbit shifts slightly away from the proton, so that these two centers are separated by a distance delta r, equation (20) expresses how much greater the pull on the proton will be than the effective push on the electron in its new orbit. This we call the gravitational force since it is an attractive force which pulls the H atom toward the source if it is free to move. We assume that it is not completely free to move but is restrained by elastic forces, somewhat equivalent to that of a spring. When the attracted atomic system is moved a distance delta r' by delta F, work is done. If we assume that delta r' is directly proportional to delta r, we then have for the work:
(Eq. 21) ?W = ?F ? ?r' = L-Qqrow2 ?r2/r2
![]()
Since there are approximately 1015 simultaneous pulls and pushes delta P each second which as a function of time would be approximately sinusoidal it should give rise to a high frequency vibratory motion which should be approximately simple harmonic in character. The polarization displacement delta r produced by the field Em should be directly proportional to its intensity. Let us assume that upon release from the pull of a single pulse the H atom would be pulled back to its original position with an elastic force negatively proportional to the displacement delta r'. We have therefore laid the foundation for a simple harmonic vibratory motion of the atom:
(Eq. 22) - ?r' = l ?r = Fqrow2/r
and
(Eq. 23) ?r2 = k' q2ro2 w4/r2

where the k values are all constants. Equation (23) in (21) gives:
(Eq. 24) delta W = K" Qq3ro3w6/r4
![]()
and since Q = q in the H atom:
(Eq. 25) delta W = K" Q4ro3 w6/ r4
![]()
For this type of motion we know that the maximum amplitude would be proportional to the square root of the total energy (25). If the maximum amplitude is proportional to the maximum value of ?F then we have:
(Eq. 26) ?Fm = K" Q2roK v3/r2
![]()
Since the phenomenon is sinusoidal, its effective value would
be delta 7o = delta 7o/sq. root 2 ![]() . If we now let
Q2 = koM1N2, the
product of the two atomic masses, and G = K"'korow3/
sq. rt. 2, we have upon replacing delta fe by simply
P:
. If we now let
Q2 = koM1N2, the
product of the two atomic masses, and G = K"'korow3/
sq. rt. 2, we have upon replacing delta fe by simply
P:
(Eq. 27) F = G M1N2/r2
![]()
which is Newton's Universal Law of Gravitation.
The foregoing derivation is obviously a very elementary and non-rigorous attempt by the author to indicate how two hydrogen atoms could conceivably attract each other by means of their motional electric fields giving rise to Newton's Universal Law of Gravity. We teach that two such atoms do attract each other according to this law. It seems reasonable therefore to expect that such a derivation as is here suggested cannot be too far from representing the electromagnetic basis behind the phenomenon.
A motional electric field is an electric field because it acts with force on electric charges. The essential ingredients of this field consist of a magnetic field, a charge of electricity and relative motion between them. It is preeminently an electromagnetic field. We have theoretically seen just how this field could very well be the vital agency which produces the attractive force we call gravity. We have also presented experimental evidence that this field possesses in common with gravity its chief property of being immune to shielding. Whether or not this field will ultimately be identified with gravity remains to be shown experimentally. We have made a closely reasoned approach to what may ultimately prove to be the missing link in a unified theory between the three great forces of nature, electricity and magnetism on the one hand and gravity on the other.
We have shown theoretically that two electromagnetic fields should emanate from all atoms, the intensity of one varying inversely with the distance and the other inversely as the cube of the distance. While these fields radiate or extend into space surrounding material atoms, there is no experimental evidence extent that these fields transmit energy by means of quanta or ions. These fields, therefore, cannot properly be defined as radiant energy any more than one can think of the motional electric field in an alternating current generator as a form of radiant energy. The modus operandi of these two fields is one of electromagnetic induction even as it is in our electric generators and motors. Persuasive and excellent reasons exist to predict that these two fields, emanating from the earth, might prove to be the source of free electric power, in a measure exceeding our present comprehension. A properly designed ultra-high frequency receiving circuit incorporating a transistor valve should by electromagnetic energy of induction not only detect but transform and convert to usable form the kinetic energy of planetary electrons in the atoms comprising the earth. This would be atomic energy in its most usable and nonpoisonous form. Through the medium of the motional electric field emanating from atoms, both gravitational dominion and free electrical power would seem to be within the possible grasp of our age.
High-sounding and speculative as the previous paragraph may sound, we have considerable evidence in support of it. In 1933 at the age of 77, Nikola Tesla predicted essentially what has just been stated:
"Ere many generations pass, our machinery will be driven by power obtainable at any point in the universe. Is this energy static or kinetic? If static, our hopes are in vain; if kinetic, and we know this for certain, then it is a mere question of time when man will succeed in attaching his machinery to the very Wheel-Work of nature."
At this point in our thesis, a recent statement by a contemporary scientist seems most timely and fitting:
"When the great innovation appears, it will almost certainly be in a muddled, incomplete, and confusing form. To the discoverer himself, it will be only half-understood; to everybody else, it will be a mystery. For any speculation which does not at first glance look crazy, there is no hope." (45 ~ Freeman Dyson: Scientific American, September 1958).
For many years the writer has known of the somewhat obscure research activities of Mr. T. Henry Moray. His claims, which appear to have been well documented, of having invented a device which would capture cosmic radiant energy continuously, to the extent of 50 kw, sounded almost crazy upon first reading. His research work on this device extends back into the period around 1926. An account of his work has been written up in several pamphlets (46 ~ T. H. Moray: The Sea of Energy in which the Earth Floats; see also: "A Revolutionary Invention", published by himself, SLC, UT). The work of Mr. Moray is of vital interest to this thesis, especially in view of the comments made by Dr. Carl Eyring (in 1925, then head of the Department of Physics of Brigham Young University) who, after examining and studying the device in operation, could come to no other conclusion but that the electrical energy was obtained (at least in part) from field energy generated "in the earth itself" (47 ~ ibid., p. 144-145). While not then understood, this conclusion of Dr. Eyring made so many years ago is now of capital interest.
Not understanding the nature of the source and form of the energy his device absorbed, and his consequent inability to explain in understandable its operation in patent applications, and his fear of losing patent rights and a fortune, have cost this man much disappointment and frustration resulting in virtually isolating him and his device from contact with those who could have been of great help. It would appear on the surface of things that Moray may well have tapped, without knowing it, either one or both of the energy sources which have been described and mathematically predicted as originating from the atoms composing the earth.
Anti-Gravity & Electrical Power
The thrilling thing about this research project is the potential possibilities it presents, for overcoming that which keeps us down, and for providing us with free electrical power! These two possibilities, levitation and electric power appear to be practical when the experimental and engineering work of making an electronic generator of, and a receiver for, the ultra-high frequency direct pulsating motional electric fields such as are emanating from the atoms in the earth. Every piece of matter on the earth is of course such a very weak generator and receiver. What is needed in this project is something somewhat analogous to what lasers have provided for radiant energy in the form of an intense beam of concentrated coherent light. Such a generator of artificially produced gravitational waves could make anti-gravity possible. Fastened to, and directly above a space platform, such a generator with its B x V field acting in the opposite direction to the earth's B x V gravity field on the already polarized atoms in the platform would proceed to depolarize them and release them from the earth's gravitational pull. A space vehicle en route to the moon passes through such a depolarized state as the gravitational attraction of the moon on it gradually becomes equal to and oppositely directed to the earth's gravity field. If sufficiently intense, the B x V field form a generator might conceivably completely depolarize a space platform and make it weightless. Further intense action by the generator might conceivable repolarize it in a reverse direction. This would cause the earth's field to then act antigravitationally upward on the platform, and with controlled speed, carry it upward with not only the generator itself and operators, but with a payload!
The possibilities of obtaining free electrical power from the earth's B x V fields appear equally exciting. Not only from stationary land installed power plant receivers, but from receivers installed on aircraft and space vehicles. The research and experimentation needed to reduce to practice this exploitation of the earth's B x V fields appears to have relatively few hurdles before it. The development of ultra-high frequency rectifiers appears to be its first requirement, and there are no roadblocks on the horizon to this accomplishment! What the consummation of this project could mean for the economic development of remote, mountainous, inaccessible regions of the earth is beyond all imagination at this time. In the light of this thesis, the new horizons in field theory herald that the heritage of mankind is dominion over all the earth!
Some Confirming Experiments
During the past two years the writer has devoted his full time to the task of producing experimental sources of B x V fields which speak for themselves. Nature has the last word in any controversy in physics and when she speaks her words are final!
A generator of a motional electric field, all electric and with no mechanical motions involved, has been built and experimentally demonstrated. This device projects its field into the space surrounding the generator. Being immune to shielding, the B x V field readily passes through the stainless steel walls of a grounded housing chamber. Surrounding the generator is mounted a cylindrical parallel plate capacitor. The outer plate is connected to a very sensitive vibrating capacitor electrometer (Keithley 640). The inner plate is connected to the other terminal of the electrometer, one terminal of which is grounded. Voltages are induces in these wires. The net result of these induced voltages is that the potential difference induced in that portion of the wire between the capacitor plates, charges these plates, and in doing so is measured by the electrometer. The generator, capacitor and electrometer are completely surrounded by a grounded electrostatic field. Housing them in a stainless steel box with a door has served this purpose very well.
Two papers describing the construction of the all-electric generator and the experiments performed with it have been presented to meetings of the American Physical Society. The abstracts and papers will be found in the appendix.
Figure 8

A simple lecture table demonstration of the pure B x V field is illustrated in Figure 8. Two short similar bars magnets are spaced apart as shown. Midway between them a long, straight insulated wire (surrounded by a grounded conducting shield), perpendicular to the paper is fixed with its terminals connected to a sensitive galvanometer placed outside the immediate vicinity of the magnets, say overhead. The resultant magnetic flux density B from the two magnets, at the wire, is zero by the principle of superposition. If the magnet on the left be given a slow uniform velocity V and the one on the right a velocity V' equal and opposite to V, then one will note a deflection of the galvanometer needle due to the pure induced B x V field acting in the wire. Note that in this simple experiment we have two sources of B x V. Both the B and the V of each source are identical in magnitude but opposite in direction; therefore, since B x V = (-B) x (-V), the products are both positive and additive. The movement of one magnet alone will be found to yield a galvanometer deflection of half that obtained when both magnets are moved simultaneously. Note also that the wire is always in a region where B = 0, but where B x V is present and active.
One of the most fascinating aspects of our discoveries is that by the use of the phenomenon of superposition of fields, electromagnetic induction can seemingly be separated from magnetic flux energy. In other words, our all-electric motional electric field generator operates without the presence of detectable magnetic flux energy as such. It is a non-inductive device. The magnetic flux intensity has been reduced to zero by the principle of superposition, and the virtual undestroyed field associated with uncancelled flux is still active and present; hence, the name "virtual" is used to describe it. It is this virtual field which produces the pure motional electric field in the space surrounding the generator. This newly discovered pure B x V field is the most unique phenomenon known to electromagnetism because it is devoid of the electrostatic and magnetic field characteristics we have hitherto known. It is a B x V field with the resultant B = 0. Its immunity to shielding gives it a stature and a character of its own, beautifully unique and isolated from all hitherto known special fields! Our generator produces nothing but this pure previously unknown field!
Perhaps the closest approach to the V phenomenon inherent in our motional electric field generator, is the toroidal transformer. In this device we are dealing with a transformer type of induced electric field caused by the growth and death of flux. It is of great interest, however, to note that the wires of the secondary windings where the field is induced may be entirely existent in a region devoid of measurable magnetic flux, since B = 0 there. This phenomenon is always of interest to students, because the induction in the wires takes place in a region of space where, by superposition of fields the resultant magnetic flux intensity is reduced to zero without in any way impairing the electromagnetic induction of the virtual flux which is operative. It is of interest to note that our research simply extends this phenomenon to include flux cutting as well as transformer types of induction where B has been reduced to zero.
It is not surprising that many physical scientists listen to this thesis with incredulity. This is not disturbing to the author. It is but the natural path of all new discovery. Nature herself bears the burden of proof and she has spoken out clearly in behalf of the uniqueness of the motional electric field. What the role of this new electric force field will be in the future development of electromagnetism is at present an open question. Our critics point to the very small values of the induced voltages we have measured in the field of our generator. The field intensity close to our generator is at present, at room temperature, approximately of the order of ~10-2 volts/meter, with a current of 30 amperes. At cryogenic temperatures, i.e., around 4.7° K, we could expect to increase the B factor in a B x V superconducting generator, consisting of 12,000 linear conductors, approximately 100 times. Our hope in achieving an intense B x V field rests, therefore, on how much we can increase the V factor in the vector product B x V. This we know could be greatly enhanced in an electronic design of our generator. We have experimentally shown that operating our present model at the temperature of dry ice, i.e., -50° C, at high current densities, approximately doubles the value of V, the electron drift velocity. Our generator is itself a unique and novel instrument for directly measuring V with considerable precision. The experimental fact that this quantity does not increase with decreasing temperature encourages us in our anticipation that in the superconducting state where all resistance to electron motion disappears that V will be very great. The author endorses the statement of Wehr and Richards (48 ~ Introductory Atomic Physics, p. 218, Addison & Wesley, 1962), "At absolute zero the atom would have no significant cross-section and electrons could streak through a conductor without encountering any resistance at all". Should very high values of V be realized in our cryogenic experiments, it is the writer's belief that a new era in gravitational dominion will be at hand.
Appendix: Summary of Experimental Work Done by Dr. Hooper
Figure 1: Diagram of Circuitry employed for generating &
measuring the motional electric field.

Figure 2: Capacitor Potential Differences measured as a function of DC current to the generator.

Figure 3: Capacitor potential differences measured as a function of AC current to the generator.
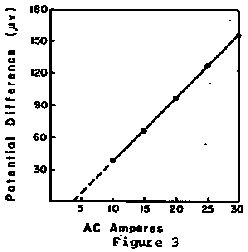
Similarities of the Motional Electric
& Gravitational Forces
W. J. Hooper
(Professor Emeritus, Principia College, President & Director of Research, Electrodynamic Gravity, Inc., PO Box 1976, Sarasota, FL
That the magnetic flux surrounding a current-carrying linear conductor moves with the electron drift velocity is demonstrated in a motional field out into the surrounding space. This field is not electrostatic. It is immune to shielding. Magnetic flux has been eliminated. The presence of this unique, special electric field is detectable and its intensity is measurable with an electrometer. From such measurements, electron drift velocities can be directly determined. The unique properties of this field strongly suggest its equivalence to the gravitational field. If equivalence proves to be a fact, then direct absorption of gravitational field energy becomes possible for electric power without pollution. If generation in great intensity becomes possible, theory indicates that the concepts of artificial gravity is space vehicles, weightlessness in limited earthly laboratories, and even anti-gravity, or lift instead of pull from the earth's gravity, have possibilities of attainment.
Introduction
How can a force like gravity originate and emanate from atoms of matter made up primarily of three elementary particles --- electrons, protons and neutrons? Einstein wrote, "It would be a great step forward if we succeeded in combining the gravitational field and the electromagnetic field into a single structure" (1). A very considerable step in this direction may have been made by the advent of the recently invented motional electric field generator and the newly revealed properties of this field. (2)
When magnetic flux is moved perpendicularly across a conductor, we say that an emf is electromagnetically induced within the conductor. This phenomenon has been little thought of as involving the production of a spacially distributed electric field. It arises from the operation called flux-cutting; wherein the electric field is motionally induced within the space occupied by the moving magnetic flux, and is present therein, whether a conductor is present in this space or not. Correctly defined, we can say that when magnetic flux of vector intensity B is moved across a region of space with vector velocity V, an electromagnetically induced electric field of vector intensity B x V makes its appearance in this space, at right angles to both B and V. For short, this induced field is called a motional electric field. A study of its properties is exciting.
Clerk Maxwell wrote in his description of the work of Michael Faraday that the intensity of the induced electric field "is entirely independent of the nature of the substance in which it acts" (3). The origin of this field, being electromagnetic induction, and non-electrostatic in nature, gives this field its penetrating nature which enables it to be present within either magnetic or non-magnetic conductors or insulators, entirely independent of the nature of the substance. The writer's extended experiments (4) involving shielding confirms Maxwell's description of this field.
The Motional Electric Field Generator
The motional electric field generator was designed and built to provide a device which would project a pure motionally induced electric field into the space surrounding it, devoid of electrostatic and magnetic accompaniments. It involves a newly discovered, non-mechanical method for moving magnetic flux, combined with one of the most basic and orthodox laws of physics, "the principle of superposition of fields". This principle states that in order to find the resultant intensity of the superimposed fields, each field should be treated as though the other is absent. The resultant is obtained by the vector addition of each field considered singly.
In 1820, Hans Christian Oersted discovered that a current-carrying conductor has magnetic flux looped about it. This discovery served to unify the then separate sciences of electricity and magnetism. In 1957, B.G. Cullwick (5), in a careful, thought-provoking analysis of moving charges, set forth three documented experimental fats to support the idea that the Oersted flux around a moving conduction electron should move with it. The writer had independently been led to the same conclusion. A plan for experimentally investigating this phenomenon was evolved. The design of the motional electric field generator was the result, and its production required the skill of an expert maker of generators and motors. This generator demonstrates and confirms that the Oersted flux actually does move with the electron drift velocity of the current giving rise to it. This discovery is a basic and fundamental contribution to electromagnetism. It also shows how this motion may possibly serve to explain the origin of gravitation from atoms of matter. The design of the generator itself will aid in seeing this possibility.
Momentarily, consider yourself in the place of a Maxwell demon, one who can see, from without, the planetary electrons of an atom orbiting about the nucleus. On the average, we may assume that there are as many going in one direction as in the opposite direction, in an approximate orbital plane. If these charges carry their Oersted magnetic fluxes with them, in the space surrounding an atom of matter, these moving fluxes will project an induced motional electric field, radially directed toward the nucleus.
The design of the motional electric field generator was such as to imitate in an elementary way the planetary electrons in an atom. The device involves no mechanically moving parts. It is wholly electrical.
The generator consists of 4020 insulated parallel linear conductors, #11, formvar insulated copper wire, nine inches in length, all connected in series and packed orderly side-by-side and tightly sealed together with epoxy into the shape of a solid, right circular cylinder. The series connections were accomplished by turning the wired through 180 degree angles without breaking the insulation. The two terminals connected to this composite of linear conductors are brought together at the axis of the cylinder and connected to a shielded and grounded two-wire cable. When energized by a direct current, 2010 conductors are at any instant carrying current and magnetic flux vertically downward, and the same number of conductors are doing the same thing vertically upward. This composite cylinder is thus non-inductive with no measurable magnetic flux surrounding it. The principle of super-position of fields shows that each of the two sets of linear conductors contributes a motional electric field directed radially inward toward the axis of the cylinder. The superimposed magnetic flux from these two sets of conductors consists of horizontal circular flux loops, half directed clockwise and the other half counter-clockwise, half moving upward and half moving downward. Thus, we have a unique condition in the space surrounding the cylinder: the resultant magnetic flux, due to superposition of fields, is zero; and the resultant motional electric field intensity is E = B1 x V1 + (-B1 x -V2) = 2B1x V1, or double the intensity attributable to one set of conductors alone, where B1 is the magnetic flux intensity due to 2010 linear conductors and V1, the electron drift velocity in, say, the positive upward direction. Although the magnetic flux energy in this device is reduced to zero, the electromagnetic induction giving rise to what we term the motional electric field has by no means been cancelled nor reduced.
The motional electric field is projected into the space surrounding our generator when the DC current therein is 30 amperes, equivalent to that which would be associated with the uncancelled magnetic flux around a single conductor carrying a current of over 120,000 amperes (4020 x 30 = 120,600 ampere turns).
Experimental Measurements
The motional electric field intensity is studied an measured by the use of a highly insulated, stainless steel cylindrical capacitor, placed around the generator, the inner cylinder of which is grounded and the outer cylinder is connected to the input head of a Keithley 640 Vibrating Capacitor Electrometer. A diagram of the circuitry employed in operating our generator is shown in Figure 1. The generator with its cylindrical capacitor about it is placed within a large grounded stainless steel cabinet. The vibrating capacitor electrometer head is also placed in the cabinet, close to the cylindrical capacitor, and connections are made to each plate. All connecting wires between the electrometer head and the galvanometer are electrostatically protected by grounded shielding. The electrometer galvanometer is outside the cabinet and has a grounding terminal for the whole electrometer system. The vibrating capacitor in the electrometer is energized by a small storage battery built into the electrometer galvanometer case. The inner capacitor cylinder, made of 1/8" stainless steel, is insulated from the generator conductors by epoxy, and forms a partial housing. The epoxy covering the two ends of the generator is covered with a heavy coat of sprayed silver and this, with the inner capacitor cylinder, forms a completely grounded electrostatic shield around it. The motional electric field, caused by the up and down movement of the slowly moving (virtual) magnetic flux loops, induces an emf in the surrounding space and in the wire connected to the electrometer head and its ground connection. The capacitor plates are thus charged, the potential difference of which is registered by the electrometer galvanometer.
The potential difference is obtained by integrating the line integral of the electric field intensity E between the capacitor plates. It is given in mks units by:
(Eq. 1) P.D. = /r1 r2 E dr = /r1r2 BxV dr = /r1r2 ?onIV dr/2 pi r
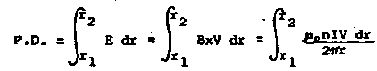
where B = ?onI/2?r webers/meter2![]() and r1
and r2 are the distances respectively from the axis
of the generator to the outer surface of the inner capacitor
plate, and the inner surface of the outside capacitor plate.
Thus, we have a typical example of how we can obtain the drift
velocity V, when r1 = 0.1 meter, r2 =
0.1035 meter, muo = 4 pi x 10-7, n =
4020, I = 10 amps, P.D. = 5 x 10-6 volts. Integrating
(1), we have:
and r1
and r2 are the distances respectively from the axis
of the generator to the outer surface of the inner capacitor
plate, and the inner surface of the outside capacitor plate.
Thus, we have a typical example of how we can obtain the drift
velocity V, when r1 = 0.1 meter, r2 =
0.1035 meter, muo = 4 pi x 10-7, n =
4020, I = 10 amps, P.D. = 5 x 10-6 volts. Integrating
(1), we have:
(Eq. 2) P.D. = muo n IV/2 pi = ?r1r2 dr/r = muo n nIV/2 pi (ln r2 - ln r1)

Solving for the drift velocity V, we have:
(Eq. 3) V = 2 pi P.D./ muonI (1n r2 - 1n r1) (meters/sec)
![]()
V = 1.78 x 10-2 meters/sec = 1.78 cm/sec
The classical derivation of the electron drift velocity is given by V = j/ne where j is the current density (j = 10/0.04172 amp/cm2), and n is the number of conduction electrons per cubic centimeter, and e is the charge on the electron (1.6021 x 10-19 coul.). Using Avogadro's number, N = 6.02252 x 1023 for calculating, n = dN/M, where d is the density, 9.96 gm/cm3, and M is the atomic weight, 63.546 gm/mole, for copper, we have
V = 239.69/(8.96 x 1022 x 1.6021 x 10-19) = 1.762 x 10-2 cm/sec. A decrease of 100-fold in n, as indicated by Fermi-Dirac statistics would bring the experimental value of the same order of magnitude as the theoretical.
Measurements of electrometer potential differences P.D. versus direct current values I, when taken quickly so as to prevent appreciable change in the temperature of the generator, due to electrical heat loss, yields a most interesting curve. Typical of most of the curves is the one shown in Figure 2. The magnitude of the motional electric field intensity will be seen to be directly proportional to the virtual value of the flux B involved, and hence to the current. The value of the electron drift velocity will also be directly proportional to the current. Thus the potential difference measured versus current values yield a parabola.
It is interesting to note that when alternating current values were plotted against electrometer deflections that a straight line was obtained instead of a parabola. This is illustrated in Figure 3.
New Research Instrumentation
When improved and perfected, this motional electric field generator, together with a capacitor and an electrometer, appear to offer unique instrumentation for directly measuring the electron drift velocity in metals. Experimental values obtained with our generator are in good agreement with accepted values. Making measurements at various temperatures will afford a method of directly determining the quantity n, the number of free conduction electrons available per nit volume, thus affording an experimental check on the Fermi-Dirac statistics method for obtaining this quantity.
Crucial Experimental Evidence
It was, of course, necessary to run down every conceivable possible source of error. The question has been raised as to whether or not the potential difference electrometer measurements that we have observed as a function of input current to our device might arise from the thermoelectric effects instead of from the assumed BxV field. It is true that at 30 amperes input, approximately 3300 watts of electrical power is being poured into our device, and it heats up at this rate, perceptibly to the hand, in a time interval of four to five minutes. It has been suggested that the juncture between the copper wire and the inner cylinder of the capacitor might be raised in temperature more rapidly than the juncture on the outer cylinder and thus give rise to an observed emf. To examine such a possibility, we have made a series of measurements requiring only a few seconds for each reading. Starting with a 30 ampere input, we have gone down to 25, and then to 20, 15 and 10, then back up the scale in 5 ampere steps to 30 and again back down to 10 amperes. The observed values of potential difference at each value of current were substantially identical. It does not seem reasonable to think that the innermost juncture could jump up and down in temperature values in a matter of seconds, permitting the electrometer galvanometer needle to return to its zero position immediately after each input value of current. When the device really warms up, each of the observed potential differences becomes enhanced and the plotted curves retain a nearly parabolic shape. We have, therefore, ruled out thermoelectric effects as giving rise to our observed measurements.
It has been suggested that possible non-cancelled magnetic fringing from the linear conductors acting on the innermost stainless steel cylinder might change the Fermi level of the metal and alter the contact differences of potential between the inner and outer cylinders of the capacitor. To eliminate this as a possible cause, a much larger diameter cylindrical capacitor was placed around the original one. The two plates of the first capacitor were grounded and measurements were made from the outermost capacitor alone.
The possibility that stray magnetic flux from the composite linear conductors, linking with the electrometer circuit, might give rise to the observed measurements was considered. A sensitive gaussmeter probe was employed to test for the existence of such flux. The maximum value found for such flux was of the order of half a gauss, found in one spot. To dispel all doubt, however, as to stray magnetic flux, a fairly large circuit, consisting of five wires was formed so that one side of the circuit came in radially from a distance of one foot to the central equatorial surface of the device, where it was held by tape and brought along parallel to the axis for several feet. This circuit loop was connected to a very sensitive microvoltmeter which was observed while various values of input current up to 30 amperes was sent into the linear conductors. No indication of an induced emf could be observed.
It is evident that the charging of the capacitor plates might possibly be due to charges carried by the current in the two wires leading onto the generator. If these wires are each at different potential differences with regard to the round, they carry an electric charge into the interior of the conducting housing enclosure of the generator and thus cause a charge of similar amount to appear on the outside of it and to produce a potential difference between the capacitor plates. This was experimentally confirmed by the inventor. When the generator housing was this raised to a positive potential difference with respect to ground, the electrometer deflections were to the right of center. When the housing was raised to a negative potential with respect to the ground, the electrometer deflections were to the left of center. These tests were made in two ways: (1) with no current flowing to the generator and 92) with current flowing, but one lead wire at a higher, or lower, potential with respect to ground than the other. Thus, it became evident that the two wires leading to the generator, with the grounded shielding, can be prevented from carrying a charge into the interior of the generator of the two wires are each constantly maintained at exactly the same value of potential difference above and below ground potential. A special power supply was built to provide this requirement. The voltage of each wire entering the generator was tested for various values of current and the potential differences were found to be accurately identical, above and below ground. Now, the deflections of the electrometer for various values of current were always to the right of center, indicating a electric field directed toward the generator was charging the plates. This field could not have come from a charge on the grounded generator housing with no net charge entering the generator, since such a possibility was carefully eliminated. Thus, the electric field must be due to the predicted B x V field. It is always directed toward the generator. This is a distinguishing characteristic of the B x V when it is due to the movement of electrons. If the current were due to the movement of positrons or protons, then the B x V field produced would be directed away from these currents instead of towards them! Alternating current thus produces electrometer deflections to the right of zero center the same as direct current, and this can be explained only in terms of the B x V. Had the electrometer deflections been due to electrostatic charging, the electrometer needle would have remained under the alternating impulses, 60 times each second, when AC current was used.
The argument has been advanced that the movement of the magnetic field with the free as well as the orbital electrons in a piece of metal would result in a considerably inwardly directed motional electric field in the space all around this metal piece, contrary to experience. Our reply to this argument is that the motional electric field, thus undoubtedly built up in the space around the metal, is in fact the weak gravitational field emanating from it. True, it has never been detected as an electric field, and we claim that this probably is due to its very high composite frequency nature. We know from gravitational experiments that there exists just such an inwardly directed force around the metal. We know that it cannot be electrostatic nor magnetic. Yet, it does emanate from an aggregate of electromagnetic sources. We have good reason to believe that in view of the immunity of the motional electric field to shielding that this field could provide the field agency for gravitation.
Electromagnetic Induction With Zero B Is Not New
Our generator somewhat resembles a properly wound toroidal coil in that, in the same space outside such a coil, carrying current, we know that B is zero due to the principle of superposition of fields. We know that when alternating current is surging back and forth in its coils that a non-electrostatic, electromagnetically induced electric field is present continuously in this space around it, where the magnetic field intensity is continuously zero. The resultant magnetic flux energy in our generator is reduced to zero while the electromagnetic induction due to the movement of virtual Oersted flux, in each of the two vertical directions, gives rise to what we call the motional electric field in the space surrounding the generator.
A simple experiment can be performed to convince one that electromagnetic induction takes place in a space where the resultant magnetic intensity has been reduced to zero by superposition of fields. With soft iron sheet, form a cylindrical magnetic shield about a meter in length and a few centimeters in diameter. A stiff wire should be held centrally within the cylindrical tube, and both tube and wire moved horizontally in a North and South direction across the vertical component of the earth's magnetic field, while the two ends of the stiff wire are connected to a sensitive galvanometer. A deflection of the galvanometer needle will readily measure the induced emf produced within the shielded wire, where the magnetic field intensity has been reduced to zero. The wire was not in motion with respect to the shielding magnetic flux induced in the shield, but it was in motion across the earth's vertical magnetic component. Now, hold the stiff horizontal wire stationary and move the cylindrical shielding horizontally at right angles to its length a permissible distance, approximately that of its inside diameter. Again a deflection of the galvanometer will measure the induced emf within the stiff wire which was stationary with respect to the earth's field, but was cut by the magnetic field within the shield, which reduced the resultant field therein to zero. If accurately measured, the emf induced in the shielded wire will be found identical for the same movement when no shield at all is employed. In one case, B = 0; in the other case, it is a real measurable value.
Mechanical Generation & Confirmation
The special distribution of motional electric field directed radially about the equatorial region of the generator was explored by means of a squirrel cage-like rotor, made up of parallel electromagnets all similarly directed so that, in some respects, it simulated the rotation of a unipolar magnet about its magnetic axis of symmetry. This apparatus is by no means such a magnet because its design is such to preclude a symmetrically uniform distribution of magnetic flux about its rotational axis. The rotation of this system of electromagnets affords an interesting experiment because here we have loops of magnetic flux of constant intensity completely filling the space about the rotor, all similarly directed from one end of the system to the other, and all in rotation about the same axis with the same angular velocity, and having a definite and constant flux pattern in space, not symmetrical nor uniform in the sense of a unipolar magnet though in a sense simulating one. That this magnetic field system rotates was readily demonstrated by means of a rectangular pickup coil placed close to the rotor and parallel to the array of electromagnets. When rotating at a speed of 10,000 rpm an AC voltage of 15 volts was obtained due to the humps of similarly directed magnetic flux which entered and left the coil. With a very sensitive zero-centered voltmeter, one could rotate the rotor by hand and demonstrate the rotation of the flux very visibly. A semi-cylindrical capacitor was next placed over the top of the rotor, with two wires centrally and radially directed (from the rotor axis) to an electrometer. In this experiment, the wires from the capacitor plates to the electrometer are cut by the unidirectionlly rotating magnetic flux which induces the motionally induced emf in this space, and is detected and measured by the DC voltage to which the capacitor plates are raised. With this apparatus one can demonstrate that rotation of the rotor in one direction yields a radial inwardly directed motional electric field, while rotation of the rotor in the opposite direction reverses the direction of the motional electric field, thus demonstrating the vector nature of the field by changing the sign of V in the vector product E = B x V, and -E = B x (-V). By keeping a constant rotation and reversing the direction of the current to the electromagnets, the direction of B can be changed while V is held constant. In this manner the direction of the motionally induced electric field can also be reversed in the surrounding space and can be made either radially inward or radially outward as evidenced by the zero-centered galvanometer needle of the Keithley 640 vibrating capacitor electrometer which was used to make the DC voltage measurements. The demonstration that a spacially distributed motional electric field exists around either our mechanical or our all-electric generator appears to us to be amply demonstrated. To be more certain, however, we obtained the services of a disinterested expert in electronics measurements to come in and check our work with a sensitive Tectronic electron oscillograph, which confirmed our observations with the Keithley Electrometer.
Relation To Relativity
The question arises as to how this new field fits into the Relativity theories? It definitely provides an interesting clarification of a hitherto speculative deduction which many relativitists have ventured to make with respect to the V x B motional electric term which enters into the transformation equations of the Special Theory as applied to electrodynamics. It has been claimed that this V x B term is electrostatic in its fundamental nature. This conclusion is now definitely shown to be incorrect by the advent of the new motional electric field generator, the field of which emanates from a grounded conducting metallic container and passes readily through any shield. The non-electrostatic nature of the V x B has also been pointed out by Winch: "Notice that the E of (E = V x B) is not an electrostatic field intensity for it is not due to a distribution of charges" (6). Nature has definitely not limited us to one type of electric field. The motional electric field is different in origin and fundamental properties from the electrostatic field arising from charges.
The writer embraces the position taken by Sir James H. Jeans in his explanation of the Special Theory of Relativity and its bearing upon the two electric fields in the transformation equations. He points out that there is nothing in the postulates of the Special Theory that requires a physical interpretation of the two electric field terms E and V x B/c in the transformation equation E' = [E - (l/c) V x B]. He states: "The equations may be taken merely as expressing relations between quantities as measured by the observer S and another S' moving with a velocity V relative to S" (7). Thus we see that there is no conflict with the Special Theory of Relativity. The philosophy of the Nobelist, P. W. Bridgman, whose "Operational Viewpoint" as set forth in his text, The Logic of Modern Physics (8), has guided the inventor in his work on this project. As Bridgman predicted, it has led to new and fundamentally basic knowledge.
That the gravitational field may possibly be identified as a motional electric field is at least very strongly suggested by the experimental work described herein. The claim of the General Theory of Relativity that the Gravitational field is equivalent to that of centrifugal force would appear to be a concept far removed form that of presenting it as a motional electric field. The experimental fact remains, however, that a pure motional electric field projected into space does simulate, in some respects, the gravitational field.
When the current flowing into this generator is constant, the motional electric field surrounding it is also constant and static, but not electrostatic, because it does not originate or terminate on charges. It readily passes through two 1/8" thick sheets, or 1/4" of stainless steel, constituting the cylindrical capacitor plates. The exciting thing about this generator is that it throws this B x V electric field out into the space around it. It is not electrostatic, not magnetic, and is immune to shielding. These properties make it a unique force in nature with possibly great utility to mankind.
Polarization & Absorption
Objects placed in this field are electrically polarized, and in making measurements of its intensity, the electrostatic fields arising from such polarization have to be reckoned with. From a well-known general theorem (9) we know that an intense convergent motional electric field would be attractive on any material object placed within it, due to this internal polarization. The recent experimental work of L. Brauner on the electric polarization due to gravity, is most interesting, as reported in the January 1969 issue of Endeavor magazine (10). His experiments convincingly show that the shoots and roots of plants when lying in a horizontal plane become electrically polarized. When turned into a vertical plane, this polarization soon disappears. Brauner presents excellent evidence in support of the conclusion that this phenomenon is due to the electrical nature of the earth's gravitational field.
This indicates in a limited way direct absorption of gravitational field energy. Of course, our hydro-electric plants are utilizing this energy in large quantities where advantageous sites for such plants can be found. The greatest potential inherent in the research described herein, the writer believes, will ultimately be in the direct absorption and conversion into useful electric power the vast reservoir of gravitational field energy which as yet has hardly been tapped. The insight into what we believe to be the mechanism within atoms which gives rise to the phenomenon of gravity, encourages us in the conviction that we can directly absorb and convert it to the service of mankind. Our research in this direction has commenced and is very encouraging.
Spacewise, this project has some speculative possibility, if and when this generated field can be made sufficiently intense. We have very considerable reason to believe that by the use of superconducting wire and liquid helium temperatures, this can be accomplished. To what extent is speculation at present, but theory would indicate that if intense fields are ever possible of generation, then the phenomenon of changing the weight of objects, and of even producing weightlessness and anti-gravity (that is, lift instead of downward pull on objects) would be possible.
Domestic and foreign patent applications covering the various generators and devies employed in our work have been field and some have been granted.
References
(1) Albert Einstein: Essays in Science, p. 10,
Philosophical Library, NY,1934.
(2) W. J. Hooper: "Equivalence of the Gravitational Field and a
Motional Electric Field"; Proceedings of the Boulder Conference
on High Energy Physics, Division of the American Physical Soc.,
Aug. 18-22, 1969, p. 483; "The Motional Electric Field
Generator"; Bull. of the American Physical Soc.,
February 1970, p. 207.
(3) Clerk Maxwell, Electricity & Magnetism, p. 181,
vol. II.
(4) W. J. Hooper: New Horizons in Electric, Magnetic &
Gravitational Field Theory, Principia College Library,
Elsah, IL.
(5) E. G. Cullwick: Electromagnetism & Relativity,
p. 245; Longsman, Green & Co., 1957.
(6) Ralph P. Winch: Electricity & Magnetism, 2nd
Edition, p. 399, Prentice Hall, Inc., 1963.
(7) J. H. Evans: Mathematical Theory of Electricity &
Magnetism, p. 606; Cambridge Univ. press, 4th Edition,
1923.
(8) P.W. Bridgman: The Logic of Modern Physics;
Macmillan Co., 1928.
(9) Jeans, op. cit., p. 125; illustrated by a block of
dielectric material being sucked in between two charged
capacitor plates.
(10) L. Brauner: "The Effect of Gravity on the Development of
Electric Potential in Plant Tisues"; Endeavor, Jan.
1969.
